Choosing the Best Model¶
Based on the previous experiments I chose Logistic Regression as the classifier to use. Given the data available, all three models have comparable F1 scores (on the test data) but the Logistic Regression classifier is the fastest for both training and prediction when compared to K-Nearest Neighbor and Random Forests. In addition, the Logistic Regression classifier offers readily interpretable coefficients and L1 regression to sparsify the data, allowing us to see the most important of the variables when deciding who will pass their final exam.
Logistic Regression works by using optimization methods to find the best parameters for a function that calculates the probability that a student’s attributes (e.g. age, school, etc.) predicts that he or she will pass the final exam. When the Logistic Regression model is created, the parameters are adjusted to maximize the f1 score, a weighted average of the model’s precision and recall.
Once the model is created, it is used to predict whether a student will pass the exam by multiplying the student’s attributes by the model’s parameters and these products are summed and added to the intercept. The resulting sum is then converted to a probability - if the probability is greater than 
the prediction will be that the student passed (passed=’yes’) otherwise it will be that the student did not pass (passed=’no’).
Fitting The Model¶
The Logistic Regression model was fit using sklearn’s GridSearchCV with 10 folds for the cross-validation. The parameters tested were the penalty-type (l1 or l2), C - the inverse of the regularization strength (the smaller the number the larger the penalty), and weights associated with each class.
The penalties refer to regularization penalties that shrink or eliminate variable-coefficients in the model. The l1 penalty refers to lasso regularization which causes some of the feature-variable coefficients to go to 0 if they don’t contribute as much to the model as the other, more significant variables. The l2 penalty refers to ridge regression which shrinks the coefficients but never pushes them all the way to 0. Since lasso regularization simplifies the model it might seem that it would be preferable, but it will only outperform ridge regression if there are differences in how much the variables contribute. If all the variables contribute equally to the model, then ridge regression will outperform the lasso (James G. et al., 2013).
C is the inverse of the regularization strength. The stronger the regularization (and thus the smaller C is), the smaller the coefficients in the model will be and for lasso the fewer the coefficients it will have. Shrinking the coefficients too much or eliminating too many variables can weaken the model so how much regularization is needed is determined here using cross-validation.
The weights used for the classes were either 1, ‘balanced’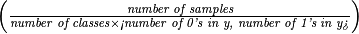 
, or 0.67 for passed and 0.33 for didn’t pass.
The following is the outcome of fitting the Logistic Regression classifier using Grid Search with the parameters given.
Parameters¶
| Parameter | Value |
|---|---|
| penalty | l1 |
| C | 0.09 |
| class_weight |
These are the parameters for the model that had the highest F1 score. The best scorer used l1 (lasso regularization) suggesting that the features contribute unequally to the outcome. The amount of regularization used was fairly high (C is the inverse of the amount of regularization, the smaller it is the more regularization there is) so the model should be fairly sparse compared relative to the number of variables in the data set. Although it looks like there was no class_weight set, this is because None was chosen, so the class weights were assumed to be 1.
Coefficients¶
| Variable | Description | Coefficient | Odds |
|---|---|---|---|
| Medu | mother’s education | 0.14 | 1.16 |
| age | student’s age | 0.03 | 1.03 |
| famrel | quality of family relationships | 0.03 | 1.03 |
| Fedu | father’s education | 0.01 | 1.01 |
| absences | number of school absences | -0.02 | 0.98 |
| goout | going out with friends | -0.07 | 0.93 |
| failures | number of past class failures | -0.46 | 0.63 |
These are the variables that remained in the best model after the regularization was applied, sorted by their coefficient-values. The coefficients are log-odds so calculating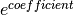 
gives you the increase in odds that the student will graduate (Peng C. et al., 2002). If the odds are greater than one, then increasing the attribute associated with the coefficient will increase the probability that the student passed and if the odds are less than one, then increasing the attribute associated with the coefficient will reduce the probability that the student passed.
Probability Plots¶
This is a plot of the various model’s probabilities. The x-axis is the normalized unique values for each variable and the y-axis is the predicted probability if all the other variables other than the one used in the line are set to zero. The actual y-values aren’t meaningful, but the relative slopes for the lines makes it easier to see how each variable is affecting the predictions.
The line slopes give a little more intuitive sense of what the coefficients in the previous table are telling us. The best predictor for failing was previous failures while the best predictor for passing was a mother’s education level.
Positive Contributions¶
Medu¶
The predictor with the greatest positive effect in the model was the amount of education the student’s mother received. According to the read-me file there are 5 levels.
| Level | Meaning |
|---|---|
| 0 | None |
| 1 | 4th Grade |
| 2 | 5th to 9th Grade |
| 3 | Secondary Education |
| 4 | Higher Education |
Looking at a plot of all the data, as the mother’s education-level goes up the proportion of those that pass goes up relative to those that don’t pass, with a large jump from Kindergarten - 4th grade to 5th - 9th grade levels .
age¶
This is the age of the student. It wasn’t immediately obvious why this would be a factor, assuming that the students are all in the same grade, but a plot of the data showed that the ages range from 15 to 22, with the oldest students not passing the final exam, and the 15-17 year olds being more proportionally represented among those who passed than those who didn’t, possibly because the older students were held back and thus were lower-performers to begin with.
famrel¶
According to the readme file famrel is a rating of the quality of family relations ranging form 1 (very bad) to 5 (excellent).
The plot seems to show that relations of above average (4 and 5) family-relations improved the likelihood of passing.
Negative Contributions¶
These are variables that decrease the odds of a student passing as their values increase.
absences¶
This is a straightforward count of the number of absences there were.
The differences are not large, but the distribution for those that didn’t pass has a greater spread and at around 10 absences the distributions seem to cross over with the non-passing line raised above the passing line (indicating a greater proportion of non-passing students).
goout¶
This is how often the student goes out with friends. There are 5 levels from 1 (very low) to 5 (very high).
It looks like going out more than the average has a negative effect on passing.
failures¶
This is the most negative variable and represents the number of past class failures for a student. It ranges from 0 to 4 with 4 meaning 4 or more failures.
It looks like no student failed 4 or more classes before taking the final exam and there were more failing students than passing students once there were any failures.
F1 score (Test Set)¶
The best F1 score for the Logistic Regression classifier was 0.86, which is a slight improvement over the default Logistic Regression classifier used earlier which had an f1 of approximately 0.81 for the test set when trained with 300 training instances.
Conclusion¶
Using Logistic Regression I found created a model with seven variables that predicts whether a student will pass or fail their final exam. There are several ways that this could have been improved. The data-sets wasn’t balanced (there were more students who passed than that didn’t pass) which might have an affect on the model. The train_test_split function has a stratify parameter that could be used to see if this makes a difference. Additionally, the data set is quite small so it’s possible that the shuffling of the data before splitting the testing and training data might have an effect. Different random-seeds should be tried to test this. Finally, the other proposed algorithms should be fitted with grid-search as well (both with the full data-sets and with the reduced, seven variable data set) to see how well they perform once their parameters are tuned.