Connected Components

1.1 Connected Graphs

An unconnected graph is connected if every pair of nodes has a path between them.

left = tuple("AAAAABBCDFFFGGGHIJKKKLLLN")
right = tuple("BECGNCDDEGIJHIJIJOLMOMNOO")
undirected = Graph()
undirected.add_edges_from(list(zip(left, right)))
draw(undirected, with_labels=True)

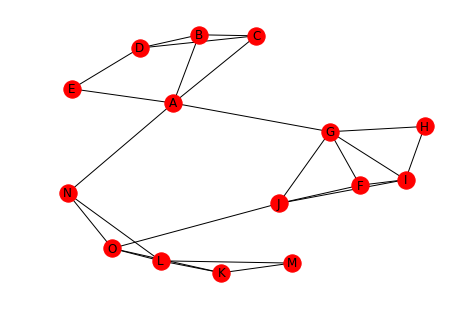
Is this graph connected? It looks like it, since every node has an edge to it.

print(networkx.is_connected(undirected))

True

To make this graph unconnected you need to remove some edges that connect sub-graphs.

undirected.remove_edges_from([("A", "G"), ("A", "N")])
draw(undirected, with_labels=True)

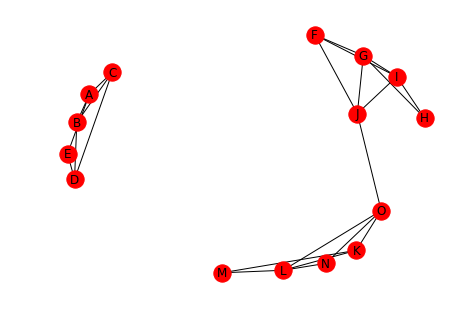
print(networkx.is_connected(undirected))

False

1.2 Connected Components

A connected component is a subset of nodes where:

• Every node in the subset has a path to every other node
• No node outside the subset has a path to a node in the subset

Let's break the graph a little more.

undirected.remove_edge("J", "O")
draw(undirected, with_labels=True)

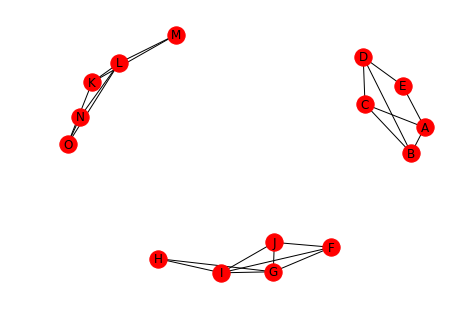
We now have three connected components.

print(networkx.number_connected_components(undirected))

3

Which we can inspect.

for component in networkx.connected_components(undirected):
    print(component)

{'J', 'I', 'G', 'H', 'F'}
{'N', 'M', 'O', 'K', 'L'}
{'D', 'B', 'C', 'E', 'A'}

We can also pick out a node from one of the components and get the sub-set.

print(networkx.node_connected_component(undirected, "A"))

{'B', 'D', 'C', 'A', 'E'}

Which you can see is the third connected component in the example above.

2.1 Strongly Connected

A strongly connected graph is a directed graph where for every pair of nodes there is a directed path in both directions.

left = tuple("AABCDD")
right = tuple("BDDBCA")

directed = DiGraph()
directed.add_edges_from(list(zip(left, right)))
draw(directed, with_labels=True)

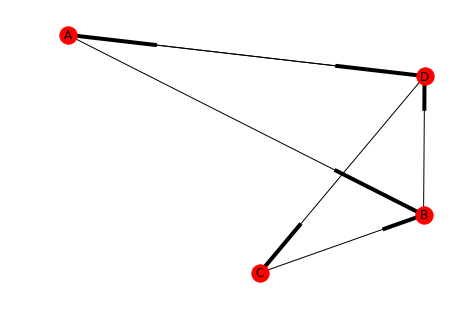
For some reason networkx uses boxes instead of arrow-heads, but hopefully you get the idea.

print(networkx.is_strongly_connected(directed))

True

2.2 Weakly Connected

A directed graph is weakly connected if, when all the edges are replaced by undirected edges (converting it to an undirected graph) then the graph is connected.

directed.remove_edge("B", "D")
print(networkx.is_strongly_connected(directed))
print(networkx.is_weakly_connected(directed))

False
True

draw(directed, with_labels=True)

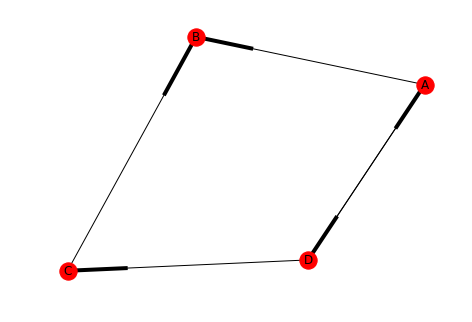
Our new graph isn't strongly connected because there's no path from B to A (or B to C, etc.). But it is weakly connected since removing the directions just makes it a loop.

2.3 Strongly Connected Component

This is a subset of nodes in a directed graph where:

• Every node in the subset has a directed path to every other node
• No node outside the subset has a directed path to and from every node in the subset

left = tuple("ADDDEFFFFGGH")
right = tuple("HBFGGABGHHCE")
directed_2 = DiGraph()
directed_2.add_edges_from(list(zip(left, right)))
draw(directed_2, with_labels=True)

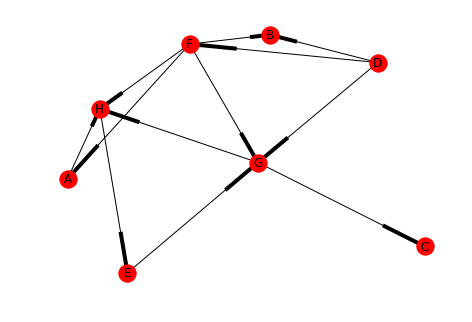
print(networkx.is_strongly_connected(directed_2))

False

You can see that the graph is not strongly connected (there's no path to E, for instance) but is there a strongly connected component within it?

for component in networkx.strongly_connected_components(directed_2):
    print(component)

{'C'}
{'H', 'G', 'E'}
{'A'}
{'B'}
{'F'}
{'D'}

In this case H, G, and E are a strongly connected component (as are each of the other individual nodes). What if we add a path from B to D?

directed_2.add_edge("B", "D")
draw(directed_2, with_labels=True)

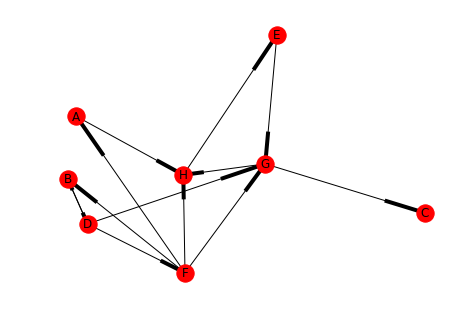
for component in networkx.strongly_connected_components(directed_2):
    print(component)

{'C'}
{'H', 'G', 'E'}
{'A'}
{'B', 'F', 'D'}

Now there are two interesting strongly connected components and two not so interesting ones.

2.4 Weakly Connected Components

A weakly connected component is one where a directed graph is converted into an undirected graph and the sub-set of nodes is a connected component.

directed_2.remove_edges_from([("F", "A"), ("F", "H"), ("F", "G"), ("D", "G"), ("B", "D"), ("E", "G")])
directed_2.add_edge("G", "E")
draw(directed_2, with_labels=True)

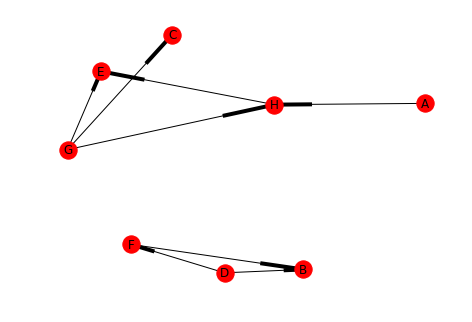
for component in networkx.strongly_connected_components(directed_2):
    print(component)

{'C'}
{'E'}
{'H'}
{'A'}
{'B'}
{'F'}
{'D'}
{'G'}

undirected_2 = directed_2.to_undirected()
draw(undirected_2, with_labels=True)

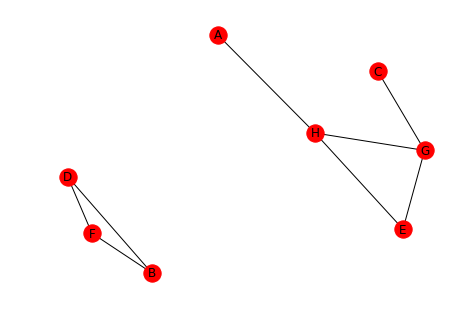
Looking at the converted graph you can see that there are two connected components.

for component in networkx.connected_components(undirected_2):
    print(component)

{'A', 'H', 'G', 'C', 'E'}
{'D', 'B', 'F'}

An important thing to note is that A and C are part of their connected component, even though visually they look like they're dangling out there.

You can also skip the conversion and let network x do it for you.

for component in networkx.weakly_connected_components(directed_2):
    print(component)

{'G', 'C', 'H', 'E', 'A'}
{'B', 'F', 'D'}