Binary Search Tree: In-Order Traversal

Source

This is the next post in a series on Binary Search Trees that start with this post.

Traversing a Tree

There are three common ways to traverse a Binary Search Tree which can be characterized by when the root of the tree is added:

  • Pre-Order Tree Walk
    1. root
    2. sub-trees
  • In-Order Tree Walk
    1. left sub-tree
    2. root
    3. right sub-tree
  • Post-Order Tree Walk
    1. sub-trees
    2. root

We're going to look at how to get the nodes of the tree in sorted (non-decreasing) order, which is a characteristic of the In-Order Tree Walk.

The Algorithm

CLRS gives the In-Order Tree Walk in the context of printing the nodes of the tree in order.

\begin{algorithm}
\caption{In-Order Tree Walk}
\begin{algorithmic}
\INPUT Node \textit{x}

\PROCEDURE{InorderTreeWalk}{\textit{x}}
\IF {\textit{x} $\neq$ \textsc{Nil}}

 \STATE \textsc{InorderTreeWalk}(\textit{x.left})
 \STATE \textsc{Print}(\textit{x.key})
 \STATE \textsc{InorderTreeWalk}(\textit{x.right})
\ENDIF
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

Implementing It

The Function

def in_order_traversal(root: Node) -> None:
    """Print the nodes in order

    Args:
     root: the root node
    """
    if root is not None:
        in_order_traversal(root.left)
        print(root, end=" ")
        in_order_traversal(root.right)
    return

A First Sample

Let's start with a simple example.

nil

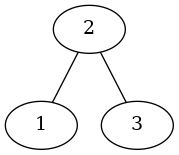
root = Node(key=2)
root.left = Node(key=1)
root.right = Node(key=3)
root.check_node()
in_order_traversal(root)

1 2 3

A Little Fancier

nil

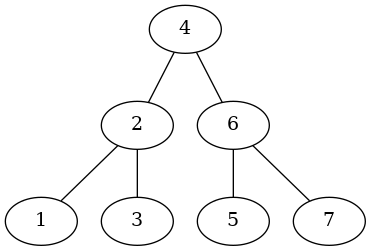
rootier = Node(key=4)
rootier.left = root
right = Node(key=6)
right.left = Node(key=5)
right.right = Node(key=7)
right.check_node()
rootier.right = right
rootier.check_node()
in_order_traversal(rootier)

1 2 3 4 5 6 7

End

The Posts

Sources