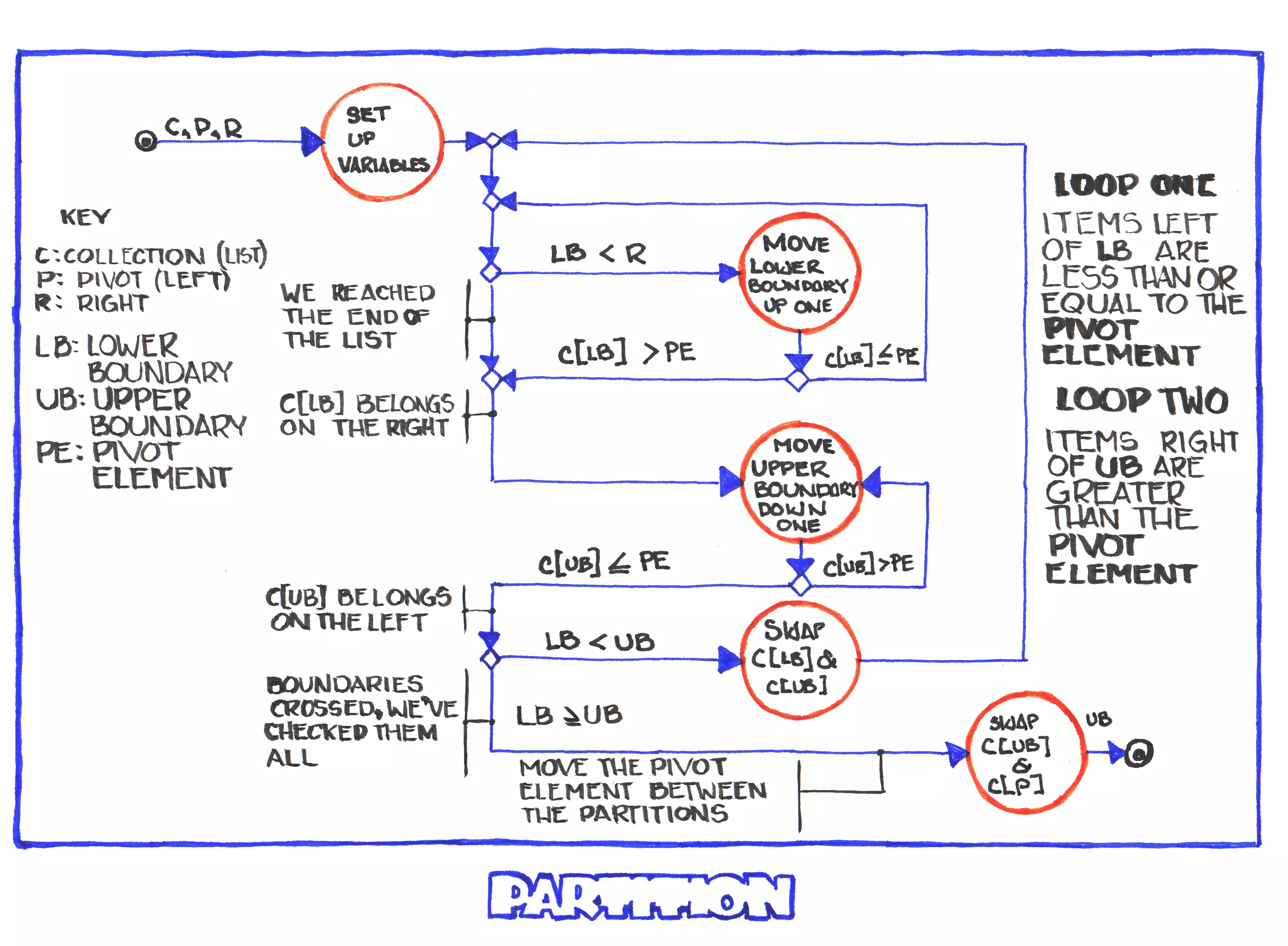
Levitin's Partition
Table of Contents
Introduction
This is part of a series that starts with this post.
The Algorithm
The Levitin version of the Partition function is a little more complicated than the CLRS version. It uses an outer loop with two inner loops. The outer loop continues until the indices for the partitions cross-over (or meet) and the inner loops move the boundaries until they find a value that needs to be swapped to the other partition (e.g. the loop sweeping upwards finds an element that's greater than or equal to the pivot element and so it needs to be moved to the upper partition). It uses the first element in the array as the value around which to partition the array.
\begin{algorithm}
\caption{Partition (Levitin)}
\begin{algorithmic}
\INPUT An array and left and right locations defining a subarray
\OUTPUT The sub-array from left to right is partitioned and the partition location is returned
\PROCEDURE{Partition}{A, left, right}
\STATE PivotElement $\gets$ A[left]
\STATE PartitionLeft $\gets$ left
\STATE PartitionRight $\gets$ right + 1
\STATE \\
\REPEAT
\REPEAT
\STATE PartitionLeft $\gets$ PartitionLeft + 1
\UNTIL {A[PartitionLeft] $\geq$ PivotElement}
\STATE \\
\REPEAT
\STATE PartitionRight $\gets$ PartitionRight - 1
\UNTIL {A[PartitionRight] $\leq$ PivotElement}
\STATE \\ Swap(A[PartitionLeft], A[PartitionRight])
\UNTIL {PartitionLeft $\geq$ PartitionRight}
\STATE \\ Swap(A[PartitionLeft], A[PartitionRight])
\STATE Swap(A[left], A[PartitionRight])
\RETURN PartitionRight
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}
The Implementation
Imports
# python
from collections.abc import MutableSequence
from functools import partial
import random
# pypi
from expects import be_true, contain_exactly, equal, expect
import altair
import pandas
# software under test
from bowling.sort.quick import levitins_partition
# monkey
from graeae.visualization.altair_helpers import output_path, save_chart
SLUG = "levitins-partition"
OUTPUT_PATH = output_path(SLUG)
save_it = partial(save_chart, output_path=OUTPUT_PATH)
The version Levitin uses appears to be closer to the version given by Tony Hoare, the creator of Quicksort. A notable difference between Wikipedia's pseudocode for Hoare's version and this version is that Hoare uses the middle element in the sub-array as the pivot while Levitin uses the left-most element as the pivot.
def partition_levitin(collection: MutableSequence,
left: int, right: int) -> int:
"""Partitions the collection around the first element
Args:
collection: the list to partition
left: index of the first element in the sub-list to partition
right: index of the last element in the sub-list to partition
Returns:
the index of the pivot element
"""
pivot_element = collection[left]
partition_left = left
partition_right = right + 1
while True:
# if the pivot element is the largest element this loop
# will try to go past the end of the list so we need a
# check in the loop before we increment the partition_left
while partition_left < right:
partition_left += 1
if collection[partition_left] >= pivot_element:
break
while True:
partition_right -= 1
if collection[partition_right] <= pivot_element:
break
if partition_left >= partition_right:
break
collection[partition_left], collection[partition_right] = (
collection[partition_right], collection[partition_left]
)
# move the pivot element from the far left to its final place
collection[left], collection[partition_right] = (
collection[partition_right], collection[left]
)
return partition_right
Some Checks
start = [8, 9, 7]
output = levitins_partition(start, 0, 2)
expect(output).to(equal(1))
expect(start).to(contain_exactly(7, 8, 9))
start = [9, 9, 9 ,9, 9]
output = levitins_partition(start, 0, 3)
expect(output).to(equal(len(start)//2))
start = [0, 1, 2, 3, 4, 5]
output = levitins_partition(start, 0, 5)
expect(output).to(equal(0))
expect(start).to(contain_exactly(0, 1, 2, 3, 4, 5))
start = [5, 4, 3, 2, 1, 0]
output = levitins_partition(start, 0, 5)
expect(output).to(equal(5))
expect(start).to(contain_exactly(0, 4, 3, 2, 1, 5))
prefix = random.choices(range(100), k=100)
middle = 100
suffix = random.choices(range(101, 201), k=100)
test = [middle] + prefix + suffix
output = levitins_partition(test, 0, len(test) - 1)
expect(output).to(equal(middle))
expect(test[output]).to(equal(middle))
expect(all(item < middle for item in test[:output])).to(be_true)
expect(all(item > middle for item in test[output + 1:])).to(be_true)
A Levitin Tracker
This is the same function (hopefully) as levitins_partition but it collects the position of the elements in the list as things get swapped around so that we can plot it.
def levitin_tracker(collection: MutableSequence,
left: int, right: int) -> tuple:
"""Partitions the collection around the last element
Args:
collection: the list to partition
left: index of the first element in the sub-list to partition
right: index of the last element in the sub-list to partition
Returns:
locations dict, lower_bounds, upper_bounds
"""
# for the plotting
locations = {value: [index] for index, value in enumerate(collection)}
upper_bound = right
lower_bound = left
lower_bounds = [lower_bound]
upper_bounds = [upper_bound]
# the algorithm
pivot_element = collection[left]
partition_left = left
partition_right = right + 1
while True:
while partition_left < right:
partition_left += 1
if collection[partition_left] >= pivot_element:
break
while True:
partition_right -= 1
if collection[partition_right] <= pivot_element:
break
if partition_left >= partition_right:
break
collection[partition_left], collection[partition_right] = (
collection[partition_right], collection[partition_left]
)
# update the plotting
upper_bounds.append(partition_right)
lower_bounds.append(partition_left)
for index, value in enumerate(collection):
locations[value].append(index)
collection[left], collection[partition_right] = (
collection[partition_right], collection[left]
)
# update the plotting
upper_bounds.append(partition_right)
lower_bounds.append(partition_left)
for index, value in enumerate(collection):
locations[value].append(index)
return locations, lower_bounds, upper_bounds
def levitin_track_plotter(locations, lower_bounds, upper_bounds, title, filename):
frame = pandas.DataFrame(locations)
re_indexed = frame.reset_index().rename(columns={"index": "Step"})
melted = re_indexed.melt(id_vars=["Step"], var_name="Element",
value_name="Location")
lower_frame = pandas.DataFrame({"Lower Bound": lower_bounds})
re_lowered = lower_frame.reset_index().rename(columns={"index": "Step"})
low_melted = re_lowered.melt(id_vars=["Step"], var_name="Element",
value_name="Location")
upper_frame = pandas.DataFrame({"Lower Bound": upper_bounds})
re_uppered = upper_frame.reset_index().rename(columns={"index": "Step"})
up_melted = re_uppered.melt(id_vars=["Step"], var_name="Element",
value_name="Location")
last_location = melted.Location.max()
elements = altair.Chart(melted).mark_line().encode(
x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
scale=altair.Scale(domain=(-1, last_location))),
color=altair.Color("Element:O", legend=None),
tooltip=["Step", "Element", "Location"]
)
lower = altair.Chart(low_melted).mark_line(color="red").encode(
x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
scale=altair.Scale(domain=(-1, last_location))),
tooltip=["Step", "Location"]
)
upper = altair.Chart(up_melted).mark_line(color="red").encode(
x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
scale=altair.Scale(domain=(-1, last_location))),
tooltip=["Step", "Location"]
)
chart = (elements + lower + upper).properties(
title=title,
width=800, height=520
)
save_it(chart, filename)
return
A Backwards Case
middle = 20
first_half = list(range(middle))
second_half = list(range(middle + 1, 2 * middle))
random.shuffle(first_half)
random.shuffle(second_half)
items = [middle] + second_half + first_half
locations, lower_bounds, upper_bounds = levitin_tracker(items, 0, len(items) - 1)
levitin_track_plotter(locations, lower_bounds, upper_bounds,
"Levitin Worst Case Swaps", "levitin-worst-plot")
A More Random Case
Let's try something a little more random.
middle = 20
first_half = list(range(middle))
second_half = list(range(middle + 1, 2 * middle))
items = first_half + second_half
random.shuffle(items)
items.append(middle)
locations, lower_bounds, upper_bounds = levitin_tracker(items, 0, len(items) - 1)
levitin_track_plotter(locations, lower_bounds, upper_bounds,
title="Randomized Input", filename="levitin-randomized-input")
A Sketch Of The Implementation