Denoising Autoencoder
Table of Contents
Sticking with the MNIST dataset, let's add noise to our data and see if we can define and train an autoencoder to de-noise the images.
Set Up
Imports
Python
from collections import namedtuple
from datetime import datetime
from pathlib import Path
PyPi
from torchvision import datasets
from graphviz import Graph
import matplotlib.pyplot as pyplot
import numpy
import seaborn
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.transforms as transforms
The Plotting
get_ipython().run_line_magic('matplotlib', 'inline')
get_ipython().run_line_magic('config', "InlineBackend.figure_format = 'retina'")
seaborn.set(style="whitegrid",
rc={"axes.grid": False,
"font.family": ["sans-serif"],
"font.sans-serif": ["Open Sans", "Latin Modern Sans", "Lato"],
"figure.figsize": (8, 6)},
font_scale=3)
The Data
The Transform
transform = transforms.ToTensor()
Load the Training and Test Datasets
path = Path("~/datasets/MNIST/").expanduser()
print(path.is_dir())
True
train_data = datasets.MNIST(root=path, train=True,
download=True, transform=transform)
test_data = datasets.MNIST(root=path, train=False,
download=True, transform=transform)
Create training and test dataloaders
NUM_WORKERS = 0
BATCH_SIZE = 20
train_loader = torch.utils.data.DataLoader(train_data, batch_size=BATCH_SIZE,
num_workers=NUM_WORKERS)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=BATCH_SIZE,
num_workers=NUM_WORKERS)
Test for CUDA
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print("Using: {}".format(device))
Using: cuda:0
Visualize the Data
Obtain One Batch of Training Images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
Get One Image From the Batch
img = numpy.squeeze(images[0])
Plot
figure, axe = pyplot.subplots()
figure.suptitle("Sample Image", weight="bold")
image = axe.imshow(img, cmap='gray')
Denoising
As I've mentioned before, autoencoders like the ones you've built so far aren't too useful in practive. However, they can be used to denoise images quite successfully just by training the network on noisy images. We can create the noisy images ourselves by adding Gaussian noise to the training images, then clipping the values to be between 0 and 1.
We'll use noisy images as input and the original, clean images as targets.
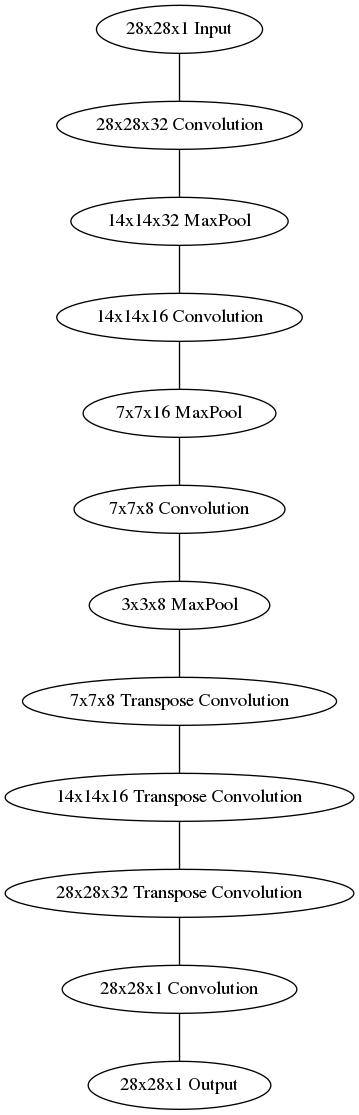
Since this is a harder problem for the network, we'll want to use deeper convolutional layers here; layers with more feature maps. You might also consider adding additional layers. I suggest starting with a depth of 32 for the convolutional layers in the encoder, and the same depths going backward through the decoder.
Define the NN Architecture
graph = Graph(format="png")
# Input layer
graph.node("a", "28x28x1 Input")
# the Encoder
graph.node("b", "28x28x32 Convolution")
graph.node("c", "14x14x32 MaxPool")
graph.node("d", "14x14x16 Convolution")
graph.node("e", "7x7x16 MaxPool")
graph.node("f", "7x7x8 Convolution")
graph.node("g", "3x3x8 MaxPool")
# The Decoder
graph.node("h", "7x7x8 Transpose Convolution")
graph.node("i", "14x14x16 Transpose Convolution")
graph.node("j", "28x28x32 Transpose Convolution")
graph.node("k", "28x28x1 Convolution")
# The Output
graph.node("l", "28x28x1 Output")
edges = "abcdefghijkl"
graph.edges([edges[edge] + edges[edge+1] for edge in range(len(edges) - 1)])
graph.render("graphs/network.dot")
graph
Layer = namedtuple("Layer", "kernel stride in_depth out_depth padding".split())
Layer.__new__.__defaults__= (0,)
def output_size(input_size: int, layer: Layer, expected: int) -> int:
"""Calculates the output size of the layer
Args:
input_size: the size of the input to the layer
layer: named tuple with values for the layer
expected: the value you are expecting
Returns:
the size of the output
Raises:
AssertionError: the calculated value wasn't the expected one
"""
size = 1 + int(
(input_size - layer.kernel + 2 * layer.padding)/layer.stride)
print(layer)
print("Layer Output: {0} x {0} x {1}".format(size, layer.out_depth))
assert size == expected, size
return size
The Encoder Layers
Layer One
INPUT_DEPTH = 1
convolution_one = Layer(kernel = 3,
padding = 1,
stride = 1,
in_depth=INPUT_DEPTH,
out_depth = 32)
INPUT_ONE = 28
OUTPUT_ONE = output_size(INPUT_ONE, convolution_one, INPUT_ONE)
Layer(kernel=3, stride=1, in_depth=1, out_depth=32, padding=1) Layer Output: 28 x 28 x 32
Layer Two
The second layer is a MaxPool layer that will keep the depth of thirty-two but will halve the size to fourteen. According to the CS 231 n page on Convolutional Networks, there are only two values for the kernel size that are usually used - 2 and 3, and the stride is usually just 2, with a kernel size of 2 being more common, and as it turns out, a kernel size of 2 and a stride of 2 will reduce our input dimensions by a half, which is what we want.
\begin{align} W &= \frac{28 - 2}{2} + 1\\ &= 14\\ \end{align} max_pool_one = Layer(kernel=2, stride=2,
in_depth=convolution_one.out_depth,
out_depth=convolution_one.out_depth)
OUTPUT_TWO = output_size(OUTPUT_ONE, max_pool_one, 14)
Layer(kernel=2, stride=2, in_depth=32, out_depth=32, padding=0) Layer Output: 14 x 14 x 32
Layer Three
Our third layer is another convolutional layer that preserves the input width and height but this time the output will have a depth of 16.
convolution_two = Layer(kernel=3, stride=1, in_depth=max_pool_one.out_depth,
out_depth=16, padding=1)
OUTPUT_THREE = output_size(OUTPUT_TWO, convolution_two, OUTPUT_TWO)
Layer(kernel=3, stride=1, in_depth=32, out_depth=16, padding=1) Layer Output: 14 x 14 x 16
Layer Four
The fourth layer is another max-pool layer that will halve the dimensions.
max_pool_two = Layer(kernel=2, stride=2, in_depth=convolution_two.out_depth,
out_depth=convolution_two.out_depth)
OUTPUT_FOUR = output_size(OUTPUT_THREE, max_pool_two, 7)
Layer(kernel=2, stride=2, in_depth=16, out_depth=16, padding=0) Layer Output: 7 x 7 x 16
Layer Five
The fifth layer is another convolutional layer that will reduce the depth to eight.
convolution_three = Layer(kernel=3, stride=1,
in_depth=max_pool_two.out_depth, out_depth=8,
padding=1)
OUTPUT_FIVE = output_size(OUTPUT_FOUR, convolution_three, 7)
Layer(kernel=3, stride=1, in_depth=16, out_depth=8, padding=1) Layer Output: 7 x 7 x 8
Layer Six
The last layer in the encoder is a max pool layer that reduces the previous layer by half (to dimensions of 3) while preserving the depth.
max_pool_three = Layer(kernel=2, stride=2,
in_depth=convolution_three.out_depth,
out_depth=convolution_three.out_depth)
OUTPUT_SIX = output_size(OUTPUT_FIVE, max_pool_three, 3)
Layer(kernel=2, stride=2, in_depth=8, out_depth=8, padding=0) Layer Output: 3 x 3 x 8
Decoders
Layer Six
This is a transpose convolution layer to (more than) double the size of the image. The image put out by the encoder is 3x3, but we want a 7x7 output, not a 6x6, so the kernel has to be upped to 3.
transpose_one = Layer(kernel=3, stride=2, out_depth=8,
in_depth=max_pool_three.out_depth)
Layer Seven
This will double the size again (to 14x14) and increase the depth to 16.
transpose_two = Layer(kernel=2, stride=2, out_depth=16,
in_depth=transpose_one.out_depth)
Layer Eight
This will double the size to 28x28 and up the depth back again to 32, the size of our original encoding convolution.
transpose_three = Layer(kernel=2, stride=2, out_depth=32,
in_depth=transpose_two.out_depth)
Layer Nine
This is a convolution layer to bring the depth back to one.
convolution_out = Layer(kernel=3, stride=1, in_depth=transpose_three.out_depth,
out_depth=1, padding=1)
The Implementation
class ConvDenoiser(nn.Module):
def __init__(self):
super().__init__()
## encoder layers ##
self.convolution_1 = nn.Conv2d(in_channels=convolution_one.in_depth,
out_channels=convolution_one.out_depth,
kernel_size=convolution_one.kernel,
padding=convolution_one.padding)
self.convolution_2 = nn.Conv2d(in_channels=convolution_two.in_depth,
out_channels=convolution_two.out_depth,
kernel_size=convolution_two.kernel,
padding=convolution_two.padding)
self.convolution_3 = nn.Conv2d(in_channels=convolution_three.in_depth,
out_channels=convolution_three.out_depth,
kernel_size=convolution_three.kernel,
padding=convolution_three.padding)
self.max_pool = nn.MaxPool2d(kernel_size=max_pool_one.kernel,
stride=max_pool_one.stride)
## decoder layers ##
## a kernel of 2 and a stride of 2 will increase the spatial dims by 2
self.transpose_convolution_1 = nn.ConvTranspose2d(
in_channels=transpose_one.in_depth,
out_channels=transpose_one.out_depth,
kernel_size=transpose_one.kernel,
stride=transpose_one.stride)
self.transpose_convolution_2 = nn.ConvTranspose2d(
in_channels=transpose_two.in_depth,
out_channels=transpose_two.out_depth,
kernel_size=transpose_two.kernel,
stride=transpose_two.stride)
self.transpose_convolution_3 = nn.ConvTranspose2d(
in_channels=transpose_three.in_depth,
out_channels=transpose_three.out_depth,
kernel_size=transpose_three.kernel,
stride=transpose_three.stride)
self.convolution_out = nn.Conv2d(in_channels=convolution_out.in_depth,
out_channels=convolution_out.out_depth,
kernel_size=convolution_out.kernel,
padding=convolution_out.padding)
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
return
def forward(self, x):
## encode ##
x = self.max_pool(self.relu(self.convolution_1(x)))
x = self.max_pool(self.relu(self.convolution_2(x)))
x = self.max_pool(self.relu(self.convolution_3(x)))
## decode ##
x = self.relu(self.transpose_convolution_1(x))
x = self.relu(self.transpose_convolution_2(x))
x = self.relu(self.transpose_convolution_3(x))
return self.sigmoid(self.convolution_out(x))
Initialize The NN
model = ConvDenoiser()
print(model)
ConvDenoiser( (conv1): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv2): Conv2d(32, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (conv3): Conv2d(16, 8, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (t_conv1): ConvTranspose2d(8, 8, kernel_size=(3, 3), stride=(2, 2)) (t_conv2): ConvTranspose2d(8, 16, kernel_size=(2, 2), stride=(2, 2)) (t_conv3): ConvTranspose2d(16, 32, kernel_size=(2, 2), stride=(2, 2)) (conv_out): Conv2d(32, 1, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) )
test = ConvDenoiser()
dataiter = iter(train_loader)
images, labels = dataiter.next()
x = test.convolution_1(images)
assert x.shape == torch.Size([BATCH_SIZE, 32, 28, 28])
print(x.shape)
x = test.max_pool(x)
assert x.shape == torch.Size([BATCH_SIZE, 32, 14, 14])
print(x.shape)
x = test.convolution_2(x)
assert x.shape == torch.Size([BATCH_SIZE, 16, 14, 14])
print(x.shape)
x = test.max_pool(x)
assert x.shape == torch.Size([BATCH_SIZE, 16, 7, 7])
print(x.shape)
x = test.convolution_3(x)
assert x.shape == torch.Size([BATCH_SIZE, 8, 7, 7])
print(x.shape)
x = test.max_pool(x)
assert x.shape == torch.Size([BATCH_SIZE, 8, 3, 3]), x.shape
x = test.transpose_convolution_1(x)
assert x.shape == torch.Size([BATCH_SIZE, 8, 7, 7]), x.shape
print(x.shape)
x = test.transpose_convolution_2(x)
assert x.shape == torch.Size([BATCH_SIZE, 16, 14, 14])
print(x.shape)
x = test.transpose_convolution_3(x)
assert x.shape == torch.Size([BATCH_SIZE, 32, 28, 28])
print(x.shape)
x = test.convolution_out(x)
assert x.shape == torch.Size([BATCH_SIZE, 1, 28, 28])
print(x.shape)
torch.Size([20, 32, 28, 28]) torch.Size([20, 32, 14, 14]) torch.Size([20, 16, 14, 14]) torch.Size([20, 16, 7, 7]) torch.Size([20, 8, 7, 7]) torch.Size([20, 8, 7, 7]) torch.Size([20, 16, 14, 14]) torch.Size([20, 32, 28, 28]) torch.Size([20, 1, 28, 28])
Training
We are only concerned with the training images, which we can get from the train_loader.
In this case, we are actually adding some noise to these images and we'll feed these noisy_imgs to our model. The model will produce reconstructed images based on the noisy input. But, we want it to produce normal un-noisy images, and so, when we calculate the loss, we will still compare the reconstructed outputs to the original images!
Because we're comparing pixel values in input and output images, it will be best to use a loss that is meant for a regression task. Regression is all about comparing quantities rather than probabilistic values. So, in this case, I'll use MSELoss. And compare output images and input images as follows:
loss = criterion(outputs, images)
Warning: I spent an unreasonable amount of time trying to de-bug this thing because I was passing in the model's parameters to the optimizer before passing it to the GPU. I don't know why it didn't throw an error, but it didn't, it just never learned and gave me really high losses. I think it's because the style of these notebooks is to create the parts all over the place so there might have been another 'model' variable in the namespace. In any case, move away from this style and start putting everything into functions and classes - especially the stuff that comes from udacity.
class Trainer:
"""Trains our model
Args:
data: data-iterator for training
epochs: number of times to train on the data
noise: factor for the amount of noise to add
learning_rate: rate for the optimizer
"""
def __init__(self, data: torch.utils.data.DataLoader, epochs: int=30,
noise:float=0.5,
learning_rate:float=0.001) -> None:
self.data = data
self.epochs = epochs
self.learning_rate = learning_rate
self.noise = noise
self._criterion = None
self._model = None
self._device = None
self._optimizer = None
return
@property
def device(self) -> torch.device:
"""CUDA or CPU"""
if self._device is None:
self._device = torch.device(
"cuda:0" if torch.cuda.is_available() else "cpu")
return self._device
@property
def criterion(self) -> nn.MSELoss:
"""Loss-calculator"""
if self._criterion is None:
self._criterion = nn.MSELoss()
return self._criterion
@property
def model(self) -> ConvDenoiser:
"""Our model"""
if self._model is None:
self._model = ConvDenoiser()
self.model.to(self.device)
return self._model
@property
def optimizer(self) -> torch.optim.Adam:
"""The gradient descent optimizer"""
if self._optimizer is None:
self._optimizer = torch.optim.Adam(self.model.parameters(),
lr=self.learning_rate)
return self._optimizer
def __call__(self) -> None:
"""Trains the model on the data"""
self.model.train()
started = datetime.now()
for epoch in range(1, self.epochs + 1):
train_loss = 0.0
for batch in self.data:
images, _ = batch
images = images.to(self.device)
## add random noise to the input images
noisy_imgs = (images
+ self.noise
* torch.randn(*images.shape).to(self.device))
# Clip the images to be between 0 and 1
noisy_imgs = numpy.clip(noisy_imgs, 0., 1.).to(self.device)
# clear the gradients of all optimized variables
self.optimizer.zero_grad()
## forward pass: compute predicted outputs by passing *noisy* images to the model
outputs = self.model(noisy_imgs)
# calculate the loss
# the "target" is still the original, not-noisy images
loss = self.criterion(outputs, images)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
self.optimizer.step()
# update running training loss
train_loss += loss.item() * images.size(0)
# print avg training statistics
train_loss = train_loss/len(train_loader)
print('Epoch: {} \tTraining Loss: {:.6f}'.format(
epoch,
train_loss
))
ended = datetime.now()
print("Ended: {}".format(ended))
print("Elapsed: {}".format(ended - started))
return
train_the_model = Trainer(train_loader)
train_the_model()
Epoch: 1 Training Loss: 0.952294 Epoch: 2 Training Loss: 0.686571 Epoch: 3 Training Loss: 0.647284 Epoch: 4 Training Loss: 0.628790 Epoch: 5 Training Loss: 0.615522 Epoch: 6 Training Loss: 0.604566 Epoch: 7 Training Loss: 0.595838 Epoch: 8 Training Loss: 0.585816 Epoch: 9 Training Loss: 0.578257 Epoch: 10 Training Loss: 0.572502 Epoch: 11 Training Loss: 0.566983 Epoch: 12 Training Loss: 0.562720 Epoch: 13 Training Loss: 0.558449 Epoch: 14 Training Loss: 0.554410 Epoch: 15 Training Loss: 0.550995 Epoch: 16 Training Loss: 0.546916 Epoch: 17 Training Loss: 0.543798 Epoch: 18 Training Loss: 0.541859 Epoch: 19 Training Loss: 0.539242 Epoch: 20 Training Loss: 0.536748 Epoch: 21 Training Loss: 0.534675 Epoch: 22 Training Loss: 0.532690 Epoch: 23 Training Loss: 0.531692 Epoch: 24 Training Loss: 0.529910 Epoch: 25 Training Loss: 0.528826 Epoch: 26 Training Loss: 0.526354 Epoch: 27 Training Loss: 0.526260 Epoch: 28 Training Loss: 0.525294 Epoch: 29 Training Loss: 0.524029 Epoch: 30 Training Loss: 0.523341 Epoch: 31 Training Loss: 0.522387 Epoch: 32 Training Loss: 0.521689 Ended: 2018-12-22 14:10:08.869789 Elapsed: 0:14:14.036518
Checking out the results
Here I'm adding noise to the test images and passing them through the autoencoder. It does a suprising great job of removing the noise, even though it's sometimes difficult to tell what the original number is.
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
# add noise to the test images
noisy_imgs = images + noise_factor * torch.randn(*images.shape)
noisy_imgs = numpy.clip(noisy_imgs, 0., 1.)
# get sample outputs
noisy_imgs = noisy_imgs.to(train_the_model.device)
output = train_the_model.model(noisy_imgs)
# prep images for display
noisy_imgs = noisy_imgs.cpu().numpy()
# output is resized into a batch of iages
output = output.view(BATCH_SIZE, 1, 28, 28)
# use detach when it's an output that requires_grad
output = output.detach().cpu().numpy()
# plot the first ten input images and then reconstructed images
fig, axes = pyplot.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(25,4))
# input images on top row, reconstructions on bottom
for noisy_imgs, row in zip([noisy_imgs, output], axes):
for img, ax in zip(noisy_imgs, row):
ax.imshow(numpy.squeeze(img), cmap='gray')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)

That did surprisingly well.