The Perceptron Algorithm
Table of Contents
The Algorithm
- Start with random weights. \(Wb\)
- Test the weights and for every misclassified point:
- create a vector with the coordinates of the point and append a 1 to it
- multiply the vector by the learning rate
- If the prediction was 0, add the vector to the weights
- If the prediction was 1, subtract the vector from the weights
- Stop when the stopping condition has been reached:
- no misclassified points
- few enough misclassified points
- you've run long enough
Imports
From PyPi
import matplotlib.pyplot as pyplot
import numpy
import pandas
import seaborn
This Project
from neurotic.tangles.data_paths import DataPath
Setup
The Plotting
%matplotlib inline
seaborn.set(style="whitegrid")
FIGURE_SIZE = (14, 12)
The Data
path = DataPath("admissions.csv")
data = pandas.read_csv(path.from_folder)
print(data.describe())
I added the labels to match the earlier admissions problem, there aren't any in the actual data set.
Here is a plot of what we need to train our Perceptron on to create a linear classifier.
figure, axe = pyplot.subplots(figsize=FIGURE_SIZE)
accepted = data[data.Label==1]
rejected = data[data.Label==0]
axe.set_title("Admissions Data")
axe.set_xlabel("Grades")
axe.set_ylabel("Test")
axe.scatter(accepted.Grades, accepted.Test, label="Accepted")
axe.scatter(rejected.Grades, rejected.Test, label="Rejected")
legend = axe.legend()
The Implementation
Set the random seed so the outcome is reproducible
numpy.random.seed(42)
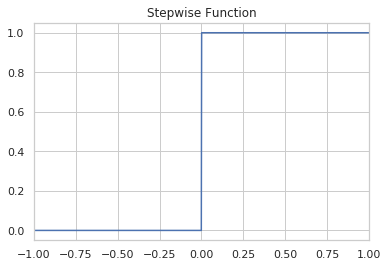
The Step Function
This is the stepwise function that decides if the output is a 1 or a 0.
\[ \hat{y} = \begin{cases} 1 \text{ if } Wx + b \geq 0\\ 0 \text{ if } Wx + b \lt 0 \end{cases} \]
def stepwise(value):
"""A function to convert the value to a label
Args:
value: number to evaluate
Returns:
label: 0 or 1 based on the value
"""
return 1 if value >= 0 else 0
figure, axe = pyplot.subplots()
axe.set_title("Stepwise Function")
axe.set_xlim((-1, 1))
x = numpy.linspace(-1, 1, 1000)
y = [stepwise(value) for value in x]
line = axe.plot(x, y)
The Prediction
\[ Wx + b = 0\\ \]
def prediction(X, W, b):
"""Predicts whether X is 0 or 1
Args:
X: matrix of inputs
W: weights
b: bias
Returns:
label: 0 or 1
"""
return stepwise((numpy.matmul(X, W) + b)[0])
The Perceptron Step
This is where the Perceptron Trick as described in the algorithm above is implemented.
def perceptron_step(X, y, W, b, learn_rate = 0.01):
"""Adjusts the weights using the Perceptron Trick
Args:
X: the input data - array of rows with two columns
y: the labels - array with one row of length matching the rows in X
W: the weights - array of shape (2, 1)
b: the bias - scalar
learn_rate: how much to adjust the weights at each step
Returns:
W,b: the new weights and bias
"""
for row in range(X.shape[0]):
predicted = prediction(X[row], W, b)
actual = y[row]
direction = actual - predicted
W = W + direction * learn_rate * W
b = b + direction * learn_rate
return W, b
The Perceptron
class Perceptron:
"""A perceptron to classify points
Args:
x_train: training data
y_train: labels for the tranining data
learnining_rate: how fast to update during training
epochs: how many times to run the training
verbosity: level of output
"""
def __init__(self, x_train: numpy.ndarray, y_train: numpy.ndarray,
learning_rate: float=0.1, epochs: int=25,
verbosity: int=0):
self.x_train = x_train
self.y_train = y_train
self.learning_rate = learning_rate
self.epochs = epochs
self.verbosity = verbosity
self._weights = None
self._bias = None
self._training_data = None
return
@property
def training_data(self) -> pandas.DataFrame:
"""the training data as a DataFrame"""
if self._training_data is None:
self._training_data = pandas.DataFrame(self.x_train)
return self._training_data
@property
def weights(self) -> numpy.ndarray:
"""Vector of weights for the predictions"""
if self._weights is None:
self._weights = numpy.array(numpy.random.rand(self.x_train[0].shape[0], 1))
return self._weights
@weights.setter
def weights(self, weights_prime: numpy.ndarray) -> None:
"""Update the weight
Args:
weights: new weights for the prediction calculations
"""
self._weights = weights_prime
return
@property
def bias(self) -> float:
"""The bias constant"""
if self._bias is None:
self._bias = numpy.random.rand(1)[0] + max(self.x_train.T[0])
return self._bias
@bias.setter
def bias(self, bias_prime: float) -> None:
"""Sets the bias for predictions"""
self._bias = bias_prime
return
def separator(self, x: float) -> float:
"""For the two-dimensional case, gives the y-value
Returns:
the y-value for the separator line
"""
return -(self.weights[0] * x + self.bias)/self.weights[1]
def predict(self, instance: numpy.ndarray) -> int:
"""makes a prediction for a single point
Args:
instance: data to make a prediction for
Returns:
prediction: a 0 or 1
"""
score = (numpy.matmul(instance, self.weights) + self.bias)[0]
return 1 if score >= 0 else 0
def take_step(self):
"""takes a single training step"""
for row in range(self.x_train.shape[0]):
predicted = self.predict(self.x_train[row])
actual = self.y_train[row]
direction = actual - predicted
self.weights = (self.weights.T
+ direction * self.learning_rate * self.x_train[row]).T
self.bias = self.bias + direction * self.learning_rate
if self.verbosity > 1:
print("Predicted: {}".format(predicted))
print("Actual: {}".format(actual))
print("Direction: {}".format(direction))
print("Weights: {}".format(self.weights))
print("Bias: {}".format(self.bias))
return
def train(self):
"""Trains the perceptron"""
if self.verbosity > 0:
print("Starting Training")
for epoch in range(1, self.epochs+1):
self.take_step()
if self.verbosity > 0:
print("Epoch: {}".format(epoch))
print("Accuracy: {}".format(self.accuracy))
return
@property
def accuracy(self) -> float:
"""What fraction of data will our current weights classify correctly"""
predictions = self.training_data.apply(lambda row: self.predict(row),
axis="columns")
correct = sum(predictions==self.y_train)
return correct/len(self.training_data)
Train the Perceptron Algorithm
This function runs the perceptron algorithm repeatedly on the dataset, and returns a few of the boundary lines obtained in the iterations for plotting purposes.
def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 25):
"""Trains the Perceptron
Args:
X: array of row-data with two-columns
y: array with labels for the row-data
learn_rate: how much to change the weights based on each data-point
num_epochs: how many times to re-train the perceptron
"""
x_max = max(X.T[0])
W = numpy.array(numpy.random.rand(2,1))
b = numpy.random.rand(1)[0] + x_max
# These are the solution lines that get plotted below.
boundary_lines = []
for i in range(num_epochs):
# In each epoch, we apply the perceptron step.
W, b = perceptron_step(X, y, W, b, learn_rate)
boundary_lines.append((-W[0]/W[1], -b/W[1]))
return boundary_lines
A Better Training
For some reason Udacity decided that giving "Try Again" as the only feedback when submitting this thing was a good idea… so I guess I'll have to do this myself. They seem to have made their stuff look much nicer than it used to, but they're still kind of tone-deaf when designing the way they structure their assignments sometimes.
epochs = 100
x_train = data[["Test", "Grades"]].values
y_train = data.Label.values
perceptron = Perceptron(x_train, y_train, epochs=epochs)
perceptron.train()
print("Accuracy after {} epochs: {}".format(epochs, perceptron.accuracy))
epochs = 1000
perceptron = Perceptron(x_train, y_train, epochs=epochs, verbosity=0)
perceptron.train()
print("Accuracy after {} epochs: {}".format(epochs, perceptron.accuracy))
figure, axe = pyplot.subplots(figsize=FIGURE_SIZE)
accepted = data[data.Label==1]
rejected = data[data.Label==0]
LIMITS = (0, 1)
axe.set_xlim(LIMITS)
axe.set_ylim(LIMITS)
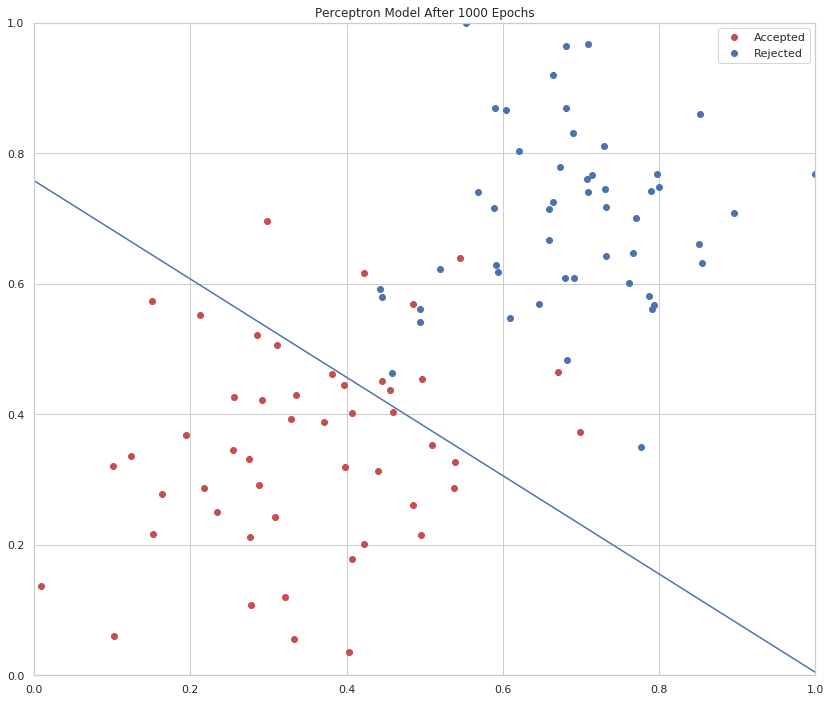
axe.set_title("Perceptron Model After {} Epochs".format(epochs))
axe.plot(accepted.Test, accepted.Grades, 'ro', label="Accepted")
axe.plot(rejected.Test, rejected.Grades, "bo", label="Rejected")
axe.plot([0, 1], [perceptron.separator(0), perceptron.separator(1)])
legend = axe.legend()