Binary Search Tree Node Insertion

This is the next post in a series on Binary Search Trees that start with this post. In this post we'll be looking at creating a Tree class and the method of inserting a node into the tree.

The Tree

Although CLRS use a T (as in tree) class in their algorithms, they only use it to store a root attribute. To make it a little more object-oriented I'll create a Tree class and add the insert method to it, rather than passing the tree to a function. Not a big change, but one that might be useful.

nil

# this project
from .node import Node
from .query import Query

class Tree:
    """Binary Search Tree

    Args:
     root: the root node for the tree
    """
    def __init__(self, root: Node=None) -> None:
        self.root = root
        self._query = None        
        return

The Query

We have kind of a chicken and the egg problem here in that I defined the Query to contain the Tree, but we need to use its min function to delete nodes. We'll see how it goes.

@property
def query(self) -> Query:
    """A Tree Query"""
    if self._query is None:
        self._query = Query(self)
    return self._query

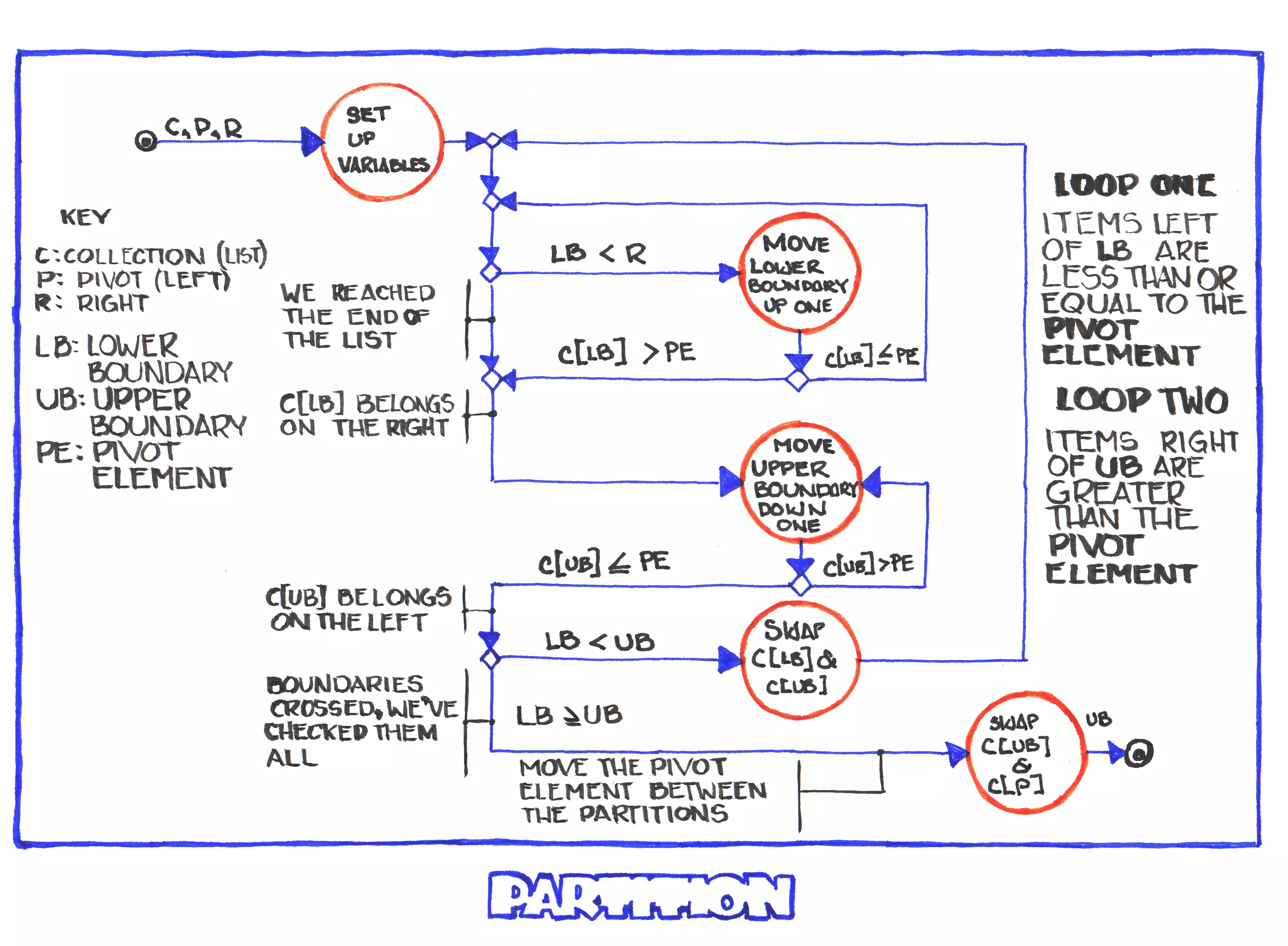
The Insertion Algorithm

This is the CLRS insert algorithm. As I noted above they consider it a function, rather than a method of the tree.

One thing that tripped me up initially was the term "insert". I thought that it would put the new node in between existing nodes, but it instead adds it as a leaf. The job of the algorithm is to find the correct leaf to add the new node to and which side to put it on (left or right).

\begin{algorithm}
\caption{Insert Node}
\begin{algorithmic}

\INPUT Tree and Node to insert.
\PROCEDURE{TreeInsert}{\textit{T, z}}

\STATE \textit{y} $\gets$ \textsc{NIL}
\STATE \textit{x} $\gets$ T.root

\WHILE {\textit{x} $\neq$ \textsc{NIL}}
 \STATE \textit{y} = \textit{x}
 \IF {\textit{z}.key < \textit{x}.key}
   \STATE \textit{x} $\gets$ \textit{x}.left
 \ELSE
   \STATE \textit{x} $\gets$ \textit{x}.right
 \ENDIF
\ENDWHILE
\STATE
\STATE \textit{z}.parent $\gets$ \textit{y}
\STATE
\IF {\textit{y} = \textsc{NIL}} 
 \STATE T.root $\gets$ \textit{z}
\ELIF {\textit{z}.key < \textit{y}.key}
  \STATE \textit{y}.left $\gets$ \textit{z}
\ELSE
  \STATE \textit{y}.right $\gets$ \textit{z}
\ENDIF

\ENDPROCEDURE

\end{algorithmic}
\end{algorithm}

What we have here is sort of a hunter and hound scenario. The hunter y is pulled along by the hound x as the hound chases down the path to find the spot for the new node. Once the hound falls into the spot where there's no node, the hunter is in the location of the leaf that should be the new node's parent and the hound is where the new node should be inserted.

The Insert Method

def insert(self, node: Node) -> None:
    """Insert the node as a new leaf in the tree

    Args:
     node: a node to insert into the tree
    """
    hunter, hound = None, self.root

    while hound is not None:
        hunter, hound = hound, hound.left if node < hound else hound.right

    node.parent = hunter

    if hunter is None:
        self.root = node
    elif node.key < hunter.key:
        hunter.left = node
    else:
        hunter.right = node
    return

from bowling.data_structures.binary_search_tree.tree import Tree
tree = Tree()

tree.insert(Node(12))
expect(tree.root).to(equal(Node(12)))

tree.insert(Node(7))
expect(tree.root.left).to(equal(Node(7)))

tree.insert(Node(20))
expect(tree.root.right).to(equal(Node(20)))

tree.insert(Node(10))
expect(tree.root.left.right).to(equal(Node(10)))

Transplant

This is an implementation of what CLRS calls Transplant (although I kind of think replace might be more to the point) where we are given two nodes - one to remove from the tree and the other to take its place. It might not seem obvious by itself why you would need it but it's used when you delete nodes.

\begin{algorithm}
\caption{Transplant Node}
\begin{algorithmic}

\INPUT Tree, Node to replace, Node to insert.
\PROCEDURE{Transplant}{\textit{T, u, v}}

\IF {\textit{u}.parent = \textsc{NIL}}
  \STATE \textit{T}.root $\gets$ \textsc{v}
\ELIF {\textit{u} = \textit{u}.parent.left}
  \STATE \textit{u}.parent.left = \textit{v}
 \ELSE
   \STATE \textit{u}.parent.right $\gets$ \textit{v}
 \ENDIF

\IF {\textit{v} $\neq$ \textsc{NIL}} 
 \STATE \textit{v}.parent $\gets$ \textit{u}.parent
\ENDIF

\ENDPROCEDURE

\end{algorithmic}
\end{algorithm}

def transplant(self, to_be_replaced: Node, replacement: Node) -> None:
    """Replace node with another

    Args:
     to_be_replaced: current holder of the position to be replaced
     replacement: node to replace the incumbent
    """
    if to_be_replaced.parent is None:
        self.root = replacement
    elif to_be_replaced == to_be_replaced.parent.left:
        to_be_replaced.parent.left = replacement
    else:
        to_be_replaced.parent.right = replacement

    if replacement is not None:
        replacement.parent = to_be_replaced.parent
    return

root = Node(50)
tree = Tree(root)
transplant = Node(666)
tree.transplant(root, transplant)
expect(tree.root).to(be(transplant))

root = Node(50)
tree = Tree(root)
lefty = Node(25)
tree.insert(lefty)

# the transplant doesn't check the Binary Search Tree Property
# before doing its thing so we have to make sure our transplant
# is less than the parent when setting the left node
smaller_transplant = Node(32)
tree.transplant(lefty, smaller_transplant)
expect(lefty.parent.left).to(equal(smaller_transplant))
expect(smaller_transplant.parent).to(be(lefty.parent))

# similarly we need to make sure the right transplant is bigger
righty = Node(42)
tree.insert(righty)
bigger_transplant = Node(48)
tree.transplant(righty, bigger_transplant)
expect(righty.parent.right).to(equal(bigger_transplant))
expect(righty.parent).to(be(bigger_transplant.parent))

Deletion

The uses for the transplant method might seem a little obscure, but it's a necessary function for our delete method to delete a node from the tree. There are three cases (four-ish really) to take care of:

  1. The node to delete has no left child: transplant the right child with the node
  2. The node to delete has no right child: transplant the left child with the node
  3. The node to delete has both children: transplant the children with the node
\begin{algorithm}
\caption{Delete Node}
\begin{algorithmic}

\INPUT Tree, Node to delete.
\PROCEDURE{Delete}{\textit{T, z}}
\IF {\textit{z}.left = \textsc{NIL}}
  \STATE \textsc{Transplant}(\textit{T, z, z.right})
\ELIF {\textit{z}.right = \textsc{NIL}}
  \STATE \textsc{Transplant}(\textit{T, z, z.left})
\ELSE
   \STATE \textit{y} $\gets$ \textsc{TreeMinimum}(\textit{z}.right)
   \IF {\textit{y}.parent $\neq$ \textit{z}}
     \STATE \textsc{Transplant}(\textit{T, y, y.right})
     \STATE \textit{y}.right $\gets$ \textit{z}.right
     \STATE \textit{y}.right.parent $\gets$ \textit{y}
   \ENDIF

  \STATE \textsc{Transplant}(\textit{T, z, y})
  \STATE \textit{y}.left $\gets$ \textit{z}.left
  \STATE \textit{y}.left.parent $\gets$ \textit{y}
\ENDIF
\ENDPROCEDURE

\end{algorithmic}
\end{algorithm}

def delete(self, node: Node) -> None:
    """Remove the node from the tree

    Args:
     node: node to remove from the tree
    """
    if node.left is None:
        self.transplant(node, node.right)
    elif node.right is None:
        self.transplant(node, node.left)
    else:
        replacement = self.query.min(node.right)
        if replacement.parent != node:
            self.transplant(replacement, replacement.right)
            replacement.right = node.right
            replacement.right.parent = replacement
        self.transplant(node, replacement)
        replacement.left = node.left
        replacement.left.parent = replacement
    return

tree = Tree(Node(50))
child = Node(25)
tree.insert(child)
left = Node(10)
right = Node(30)

tree.insert(right)
expect(tree.root.left).to(be(child))
tree.delete(child)
expect(tree.root.left).not_to(be(child))
expect(tree.root.left).to(be(right))

tree = Tree(Node(50))
child = Node(25)
tree.insert(child)
left = Node(10)
right = Node(30)
tree.insert(left)
tree.delete(child)
expect(tree.root.left).to(be(left))

root = Node(50)
tree = Tree(root)
child = Node(25)
tree.insert(child)
left = Node(10)
right = Node(30)
tree.insert(left)
tree.insert(right)
tree.delete(root)
expect(tree.root).to(be(child))

root = Node(50)
tree = Tree(root)
child = Node(25)
tree.insert(child)
left = Node(10)
right = Node(30)
tree.insert(left)
tree.insert(right)
tree.delete(child)
expect(tree.root.left).to(be(right))

Plotting

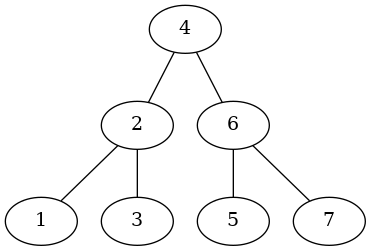
tree = Tree(Node(10))
for key in (5, 2, 3, 1, 7, 6, 8, 15, 12, 11, 14, 17, 16, 20):
    tree.insert(Node(key))
adjacencies = dict()

def inorder(node: Node, adjacencies: dict) -> dict:
    """Traverse the nodes and build an adjancency dictionary
    """
    if node is not None:
        inorder(node.left, adjacencies)
        left = node.left.key if node.left else None
        right = node.right.key if node.right else None
        if any((left, right)):
            if left and right:
                adjacencies[node.key] = (left, right)
            elif left and not right:
                adjacencies[node.key] = (left, )
            else:
                adjacencies[node.key] = (right,)
            inorder(node.right, adjacencies)
    return

inorder(tree.root, adjacencies=adjacencies)
print(adjacencies)

{2: (1, 3), 5: (2, 7), 7: (6, 8), 10: (5, 15), 12: (11, 14), 15: (12, 17), 17: (16, 20)}

Now that we have an adjacency list, let's try and plot it.

import networkx

SLUG = "binary-search-tree-node-insertion"
OUTPUT = f"files/posts/{SLUG}/"

graph = networkx.DiGraph(adjacencies)

pygraph = networkx.nx_pydot.to_pydot(graph)
pygraph.write_png(OUTPUT + "first_tree.png")

nil

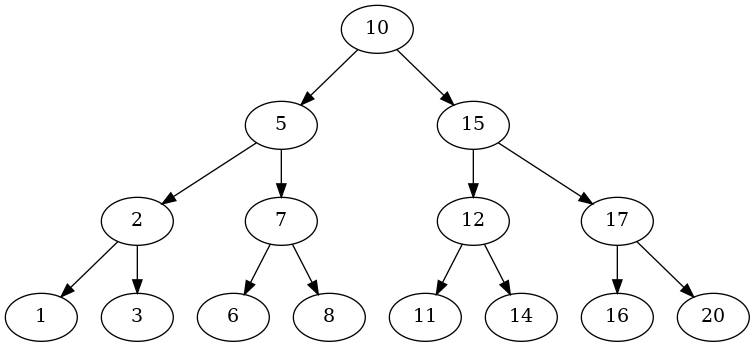
This is sort of an artificial example in that in order to get the plot right I had to insert nodes until they all had two (except the leaves), but it hopefully shows that it works.

Sources

Binary Search Tree Node

This is the next post in a series on Binary Search Trees that start with this post.

The Abstract

As mentioned in the first post, the Binary Search Tree is a linked structure made up of Nodes that look more or less like this:

nil

And which maintain the Binary Search Tree Property. I'm going to forego the data field and add a couple of methods to make it more convenient for me, but most of the way this will work will be to pass nodes (particularly the root) to functions.

The Implementation

Since I'm using pypy 3.7 there's a problem with the declaration of an attribute of the Node class being a Node object (it isn't defined yet) but according to this post on stackoverflow we can import annotations from the future to fix it.

# python
from __future__ import annotations

# this project
from bowling.types import Orderable

class Node:
    """A Node in a Binary Search Tree

    Args:
     key: item to compare nodes
     parent: parent of this node
     left: left child
     right: right child
    """
    def __init__(self, key: Orderable, parent: Node=None,
                 left: Node=None, right: Node=None) -> None:
        self.key = key
        self._parent = None
        self.parent = parent
        self._left = None
        self.left = left
        self._right = None
        self.right = right
        return

Properties

Parent

@property
def parent(self) -> Node:
    """The parent of this node"""
    return self._parent

@parent.setter
def parent(self, parent_: Node) -> None:
    """Sets the parent and updates the parent

    Warning:
     this will clobber the parent's child if there's a node where this should
    be

    Args:
     parent: to add to self

    Raises:
     AssertionError if parent and self have same key
    """
    if parent_ is None:
        self._parent = parent_
        return

    if self == parent_:
        raise AssertionError(f"Self ({self}) cannot equal parent ({parent_})")

    # since the left and right assignments update the parent
    # we need a hack to get around the setters or you end up
    # with an infinite loop - we set left, they set parent, we set left,...
    if self < parent_:
        parent_._left = self
    else:
        parent_._right = self

    self._parent = parent_        
    return

Left

@property
def left(self) -> Node:
    """The left child"""
    return self._left

@left.setter
def left(self, new_left: Node) -> None:
    """Sets the left and its parent

    Raises:
     AssertionError if left isn't less than self

    Args:
     new_left: a node to be the left child or None
    """
    if new_left is None:
        self._left = new_left
        return

    assert new_left < self, f"Left ({new_left} not < self {self})"
    new_left.parent = self
    self._left = new_left
    return

Right

@property
def right(self) -> Node:
    """The right child"""
    return self._right

@right.setter
def right(self, new_right: Node) -> None:
    """Sets the right and its parent

    Raises:
     AssertionError if right isn't greater than self

    Args:
     new_right: a node to be the right child or None
    """
    if new_right is None:
        self._right = new_right
        return

    assert new_right > self, f"right ({new_right} not > self ({self})"
    new_right.parent = self
    self._right = new_right
    return

Comparisons

These are convenience methods to make it so that you can compare the node-objects without referring to the key (see the python Data Model documentation). In reading the documentation I thought that you had to implement everything, but after implementing less than and less than or equal to the greater than and greater than or equal to comparisons started to work. I guess if you don't implement them they just take the negative of the less than cases.

Equal

def __eq__(self, other: Node) -> bool:
    """Check if the other node has an equal key

    """
    return type(self) == type(other) and self.key == other.key

Less Than

def __lt__(self, other: Node) -> bool:
    """See if this key is less than the other's

    Raises:
     TypeError: the other thing doesn't have a key
    """
    if not type(self) == type(other):
        raise TypeError(f"'<' not supported between '{type(self)}' "
                        "and '{type(other)}'")
    return self.key < other.key

Less Than or Equal

def __le__(self, other: Node) -> bool:
    """See if this key is less than or equal to other's"""
    if not type(self) == type(other):
        raise TypeError(f"'<' not supported between '{type(self)}' "
                        "and '{type(other)}'")
    return self.key <= other.key

Check Nodes

This is a convenience method to check if a node and its sub-trees maintain the Binary Search Tree Property. It calls the children too so that the whole tree can be checked by calling this on the root. Now that there's checks when the attributes are set this isn't quite as necessary. The only time you might need it is if the attributes are set directly instead of using the setter.

Note: Although the Binary Search Tree Property allows duplicate keys, once you start doing things with the tree like inserting and deleting nodes it causes problems. Also, it's not likely that the keys are what you would be most interested in when using a tree, it would be the data associated with the node, so what would it mean to have two different items associated with the same key? There are probably uses for this, but to make it simpler I'm going to treat the keys more like dictionary keys and say that it's a mistake to have duplicates.

def check_node(self) -> None:
    """Checks that the Binary Search Tree Property holds

    Raises:
     AssertionError: Binary Search Tree Property violated or duplicates exist
    """
    assert self.parent is None or type(self.parent) is Node,\
        f"self.parent={self.parent}, type={type(self.parent)}"
    if self.left is not None:
        assert self.left < self, f"Left: {self.left} not < Self: {self}"
        self.left.check_node()

    if self.right is not None:
        assert self.right > self, f"Right: {self.right} not > Self: {self}"
        self.right.check_node()
    return

String Output

This is to make it a little easier to print.

def __str__(self) -> str:
    """The key as a string"""
    return str(self.key)

Testing

I'll have to break this up later.

Imports

# pypi
from expects import (
    be_above,
    be_above_or_equal,
    be_below,
    be_below_or_equal,
    be_none,
    equal,
    expect,
    raise_error
)

# software under test
from bowling.data_structures.binary_search_tree.node import Node

One Node

parent = Node(key=10)
parent.check_node()

expect(parent.key).to(equal(10))
expect(parent.left).to(be_none)
expect(parent.right).to(be_none)
expect(parent.parent).to(be_none)

Check the Comparisons

uncle = Node(key=9)

expect(uncle).to(equal(Node(key=9)))
expect(uncle).to(be_below(parent))
expect(uncle).to(be_below_or_equal(parent))

brother = Node(key=20)

expect(brother).to(be_above(parent))
expect(brother).to(be_above_or_equal(parent))

# I'm still deciding who's responsible for checking if a node exists
# for now I'll copy what happens when None is compared to ints
expect(brother).not_to(equal(uncle.parent))

expect(lambda: brother < uncle.parent).to(raise_error(TypeError))
expect(lambda: brother.parent > uncle).to(raise_error(TypeError))

Check the Two-Way Updates.

  • Set the Parent

    In the constructor.

    parent = Node(key=10)

left = Node(5, parent=parent)
expect(left.parent).to(equal(parent))
expect(parent.left).to(equal(left))

right = Node(15, parent=parent)
expect(right.parent).to(equal(parent))
expect(parent.right).to(equal(right))

def bad_parent():
    left = Node(key=10, parent=Node(10))
    return

expect(bad_parent).to(raise_error(AssertionError))

    On the object

    parent = Node(key=10)
left = Node(5)
left.parent = parent

expect(left.parent).to(equal(parent))
expect(parent.left).to(equal(left))

right = Node(15)
right.parent = parent
expect(right.parent).to(equal(parent))
expect(parent.right).to(equal(right))

def bad_parent():
    parent = Node(key=10)
    left = Node(key=10)
    left.parent = parent
    return

expect(bad_parent).to(raise_error(AssertionError))
  • Set The Left Child
    left = Node(5)
parent = Node(key=10, left=left)

expect(parent.left).to(equal(left))
expect(left.parent).to(equal(parent))

parent = Node(key=10)
parent.left = left
expect(parent.left).to(equal(left))
expect(left.parent).to(equal(parent))
  • Set The Right Child
    right = Node(15)
parent = Node(key=10, right=right)

expect(parent.right).to(equal(right))
expect(right.parent).to(equal(parent))

parent = Node(key=10)
parent.right = right
expect(parent.right).to(equal(right))
expect(right.parent).to(equal(parent))

The Check Node Method

uncle = Node(key=9)
parent = Node(key=10)
parent.check_node()

# parent is root
expect(parent.check_node).not_to(raise_error)

# parent is right child
parent.parent = uncle
expect(parent.check_node).not_to(raise_error)

# parent is left child
parent.parent = brother
expect(parent.check_node).not_to(raise_error)

def bad_check():
    parent.check_node()
    return

# left node is greater than the parent
lefty = Node(15)
def bad(): 
    parent.left = lefty
expect(bad).to(raise_error(AssertionError))
parent._left = lefty
expect(bad_check).to(raise_error(AssertionError))

# left node is less than the parent
parent.left = None
parent.right = lefty
expect(parent.check_node).not_to(raise_error(AssertionError))

# right node is less than the parent
righty = Node(key=2)
def bad():
    parent.right = righty
    return
expect(bad).to(raise_error(AssertionError))
parent._right = righty
expect(bad_check).to(raise_error(AssertionError))

# right and left are okay
parent.left = righty
parent.right = lefty
expect(parent.check_node).not_to(raise_error)

parent = Node(key=10)
parent.left = Node(key=2)
# children of parent's children
def bad():
    parent.left.left = Node(key=100)
expect(bad).to(raise_error(AssertionError))

parent.left.left = Node(key=0)
expect(parent.check_node).not_to(raise_error)

def bad():
    lefty.right = Node(key=0)
expect(bad).to(raise_error(AssertionError))

# disallow duplicates
parent = Node(10)
def bad():
    parent.left = Node(10)
expect(bad).to(raise_error(AssertionError))

parent.key = 11
expect(bad_check).not_to(raise_error(AssertionError))

def bad():
    parent.right = Node(11)
expect(bad).to(raise_error(AssertionError))

parent.right = Node(12)
expect(bad_check).not_to(raise_error(AssertionError))

expect(str(parent)).to(equal(str(parent.key)))

The next post will be about traversing the tree in the order of the nodes.

Binary Search Tree: In-Order Traversal

This is the next post in a series on Binary Search Trees that start with this post.

Traversing a Tree

There are three common ways to traverse a Binary Search Tree which can be characterized by when the root of the tree is added:

  • Pre-Order Tree Walk
    1. root
    2. sub-trees
  • In-Order Tree Walk
    1. left sub-tree
    2. root
    3. right sub-tree
  • Post-Order Tree Walk
    1. sub-trees
    2. root

We're going to look at how to get the nodes of the tree in sorted (non-decreasing) order, which is a characteristic of the In-Order Tree Walk.

The Algorithm

CLRS gives the In-Order Tree Walk in the context of printing the nodes of the tree in order.

\begin{algorithm}
\caption{In-Order Tree Walk}
\begin{algorithmic}
\INPUT Node \textit{x}

\PROCEDURE{InorderTreeWalk}{\textit{x}}
\IF {\textit{x} $\neq$ \textsc{Nil}}

 \STATE \textsc{InorderTreeWalk}(\textit{x.left})
 \STATE \textsc{Print}(\textit{x.key})
 \STATE \textsc{InorderTreeWalk}(\textit{x.right})
\ENDIF
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

Implementing It

The Function

def in_order_traversal(root: Node) -> None:
    """Print the nodes in order

    Args:
     root: the root node
    """
    if root is not None:
        in_order_traversal(root.left)
        print(root, end=" ")
        in_order_traversal(root.right)
    return

A First Sample

Let's start with a simple example.

nil

root = Node(key=2)
root.left = Node(key=1)
root.right = Node(key=3)
root.check_node()
in_order_traversal(root)

1 2 3

A Little Fancier

nil

rootier = Node(key=4)
rootier.left = root
right = Node(key=6)
right.left = Node(key=5)
right.right = Node(key=7)
right.check_node()
rootier.right = right
rootier.check_node()
in_order_traversal(rootier)

1 2 3 4 5 6 7

End

The Posts

Sources

Binary Search Trees

What is a Binary Search Tree?

Using CLRS:

  • A Binary Search Tree is a linked structure of Nodes
  • Each Node is an object
  • Each node has a Key (and Data)
  • Each Node has Left, Right, and Parent attributes which point to the Left Child, Right-Child, and Parent of the Node.
  • If a child is missing then it is set to Nil.
  • The root Node is the only Node with a Parent set to Nil.

When describing Binary Search Trees I'll tend to refer to the Nodes but mean the Nodes' keys (e.g. to say a Node is less than another means its key is less than the other Node's).

The Binary Search Tree Property

All the nodes in the left sub-tree of a node are less than or equal to the node and all the nodes in the right sub-tree of the node are greater than or equal to the node.

Randomized Partition

Introduction

This is part of a series about the Partition algorithm that starts with this post.

Imports and Setup

# python
# For python 3.9 and newer you want to import 
# the typing classes from collections.abc
# But Ubuntu 21.10 has pypy 3.7 which needs the version from typing
# for what we want here
from functools import partial
from typing import Callable, MutableSequence, TypeVar

import random

# pypi
from expects import be_true, contain_exactly, equal, expect

import altair
import pandas

# software under test
from bowling.sort.quick import (clrs_partition,
                                levitins_partition,
                                randomized_partition)

# monkey
from graeae.visualization.altair_helpers import output_path, save_chart

SLUG = "randomized-partition"
OUTPUT_PATH = output_path(SLUG)
save_it = partial(save_chart, output_path=OUTPUT_PATH)
Orderable = TypeVar("Orderable")

The Algorithm

The randomized partition just swaps the pivot element for a random element, but since the CLRS version uses the last element as the pivot and the Levitin version uses the first element (and Hoare used the middle) I'm going to pass in the pivot and the function explicitly so I don't have to implement different versions of the randomized partition.

For the pseudocode I'll just assume that the partition function is in the global space instead of passing it in.

\begin{algorithm}
\caption{Randomized Partition}
\begin{algorithmic}
\INPUT An array and left, right, and pivot locations
\OUTPUT The sub-array from left to right is partitioned and the partition location is returned

\PROCEDURE{RandomizedPartition}{A, left, right, pivot}

\STATE i $\gets$ \textsc{Random}(left, right)
\STATE \textsc{Swap}(A[i], A[pivot])
\RETURN \textsc{Partition}(A, left, right)
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

The downside to this approach is that to use it you have to remember where the pivot is. Maybe I'll make separate ones for the different algorithms later…

The Implementation

def partition_randomized(collection: MutableSequence[Orderable],
                         left: int, right: int,
                         pivot: int,
                         partition: Partition) -> int:
    """Partitions the collection around a random element in the list

    Args:
     collection: the list to partition
     left: index of the first element in the sub-list to partition
     right: index of the last element in the sub-list to partition
     pivot: location of the pivot element
     partition: the partition function to use

    Returns:
     the index of the pivot element
    """
    random_index = random.randrange(left, right + 1)
    collection[pivot], collection[random_index] = (collection[random_index],
                                                   collection[pivot])
    return partition(collection, left, right)

Some Checks

randomized_clrs = partial(randomized_partition, pivot=-1,
                          partition=clrs_partition)
randomized_levitin = partial(randomized_partition, pivot=0,
                             partition=levitins_partition)

def test_partitioner(partitioner: Callable[[MutableSequence[Orderable], int, int], int],
                     input_size: int=10**5) -> None:
    elements = list(range(input_size))
    random.shuffle(elements)

    pivot = partitioner(elements, left=0, right=input_size-1)
    pivot_element = elements[pivot]
    expect(all(element < pivot_element
               for element in elements[:pivot])).to(be_true)
    expect(all(element > pivot_element
               for element in elements[pivot + 1:])).to(be_true)
    expect(len(elements)).to(equal(input_size))
    return

test_partitioner(randomized_clrs)
test_partitioner(randomized_levitin)

Sources

Comparing the Partition Swaps

Introduction

This is part of a series of posts about the Partition algorithm that starts with this post.

Imports and Setup

# python
from typing import Callable, List, TypeVar, MutableSequence
from dataclasses import dataclass
from functools import partial

import random

# pypi
from expects import be_true, equal, expect
from joblib import Parallel, delayed

import altair
import pandas

# monkey
from graeae.visualization.altair_helpers import output_path, save_chart

SLUG = "comparing-the-partition-swaps"
OUTPUT_PATH = output_path(SLUG)
save_it = partial(save_chart, output_path=OUTPUT_PATH)

Orderable = TypeVar("Orderable")
random.seed(2022)

Comparing the Swaps

Both of the versions of partition shown here traverse the collection once, so looking at the number of comparisons doesn't seem so interesting. According to the Wikipedia page on Quicksort, the swaps for Hoare's method (which is slightly different from Levitin's) is better for the worst cases, so let's see if this matters for Levitin's and CLRS's swaps.

Some Swap Counters

Since we're only calling the partitioners once rather than repeatedly using them to partition sub-lists in the collection we can get rid of the left and right arguments to the functions.

A Levitin Swap Counter

def levitin_swaps(collection: MutableSequence[Orderable]) -> int:
    """Partitions the collection using a variation of Hoare's method

    Args:
     collection: the list to partition

    Returns:
     count of swaps
    """
    left, right = 0, len(collection) - 1
    pivot_element = collection[left]
    partition_left = left
    partition_right = right + 1
    stop_right = len(collection) - 1
    swaps = 0
    while True:
        while partition_left < stop_right:
            partition_left += 1
            if collection[partition_left] >= pivot_element:
                break

        while True:
            partition_right -= 1
            if collection[partition_right] <= pivot_element:
                break

        if partition_left >= partition_right:
            break

        collection[partition_left], collection[partition_right] = (
            collection[partition_right], collection[partition_left]
        )
        swaps += 1

    # move the pivot element from the far left to its final place
    collection[left], collection[partition_right] = (
        collection[partition_right], collection[left]
    )
    swaps += 1
    return swaps

middle = 100
prefix = random.choices(range(middle), k=middle)
suffix = random.choices(range(middle + 1, 201), k=middle)
test = [middle] + prefix + suffix

swaps = levitin_swaps(test)

expect(all(item < middle for item in test[:middle])).to(be_true)
expect(all(item > middle for item in test[middle + 1:])).to(be_true)

A CLRS Swap Counter

def clrs_swaps(collection: MutableSequence[Orderable]) -> int:
    """Partitions the collection around the last element

    Args:
     collection: the list to partition

    Returns:
     count of swaps
    """
    left, right = 0, len(collection) - 1
    pivot_element = collection[right]
    lower_bound = left - 1
    swaps = 0
    for upper_bound in range(left, right):
        if collection[upper_bound] <= pivot_element:
            lower_bound += 1
            (collection[lower_bound],
             collection[upper_bound]) = (collection[upper_bound],
                                         collection[lower_bound])
            swaps += 1
    pivot = lower_bound + 1
    (collection[pivot],
     collection[right]) = (collection[right],
                           collection[pivot])
    swaps += 1
    return swaps

middle = 100
prefix = random.choices(range(middle), k=middle)
suffix = random.choices(range(middle + 1, 201), k=middle)
test = prefix + suffix + [middle]

swaps = clrs_swaps(test)

expect(all(item < middle for item in test[:middle])).to(be_true)
expect(all(item > middle for item in test[middle + 1:])).to(be_true)

A Parallelizer Function

This is what I'll pass to joblib to run the two swap-counter functions.

@dataclass
class SwapCounts:
    size: int
    swaps: int

def swap_counter(collection: MutableSequence, swap_counter: object) -> SwapCounts:
    """Runs the swap_counter over the collection of inputs

    Args:
     collection: elements to partition

    Returns:
     SwapCounts: size, swap-count
    """
    size = len(collection)
    swaps = swap_counter(collection)
    return SwapCounts(size=size, swaps=swaps)

def swap_plots(first_output: List[SwapCounts], second_output: List[SwapCounts],
               first_label: str, second_label: str,
               title: str, filename: str):
    """Plot the swap counts

    Args:
     first_output, second_output: lists of SwapCounts
     first_label, second_label: Algorithm labels for the counts
     title: title for the plot
     filename: name to save the plot to 
    """
    expect(len(first_output)).to(equal(len(second_output)))
    frame = pandas.DataFrame({
        "Input Size": [output.size for output in first_output],
        first_label: [output.swaps for output in first_output],
        second_label: [output.swaps for output in second_output]})

    melted = frame.melt(id_vars="Input Size",
                        value_vars=[first_label, second_label],
                        var_name="Algorithm", value_name="Swaps")

    base = (altair.Chart(melted).mark_circle(opacity=0.5)
            .encode(x=altair.X("Input Size:Q",
                               scale=altair.Scale(
                                   domain=(0, melted["Input Size"].max()))),
                    y=altair.Y("Swaps:Q",scale=altair.Scale(domainMin=0)),
                               color="Algorithm:N",
                    tooltip=[altair.Tooltip("Input Size:Q", format=","),
                             altair.Tooltip("Swaps:Q", format=","),
                             altair.Tooltip("Algorithm:N")]))

    line = (base.transform_regression("Input Size", "Swaps",
                                      groupby=["Algorithm"])
            .mark_line())
    chart = (line + base).properties(
        title=title,
        width=800,
        height=525
    ).interactive()

    save_it(chart, filename)
    return

def swap_ratio_plots(first_output: List[SwapCounts], second_output: List[SwapCounts],
                     first_label: str, second_label: str,
                     title: str, filename: str):
    """Plot the swap count ratios

    Args:
     first_output, second_output: lists of SwapCounts
     first_label, second_label: Algorithm labels for the counts
     title: title for the plot
     filename: name to save the plot to 
    """
    expect(len(first_output)).to(equal(len(second_output)))
    frame = pandas.DataFrame({
        "Input Size": [output.size for output in first_output],
        first_label: [output.swaps for output in first_output],
        second_label: [output.swaps for output in second_output]})

    frame["Ratio"] = frame[first_label]/(frame[second_label] + 1)

    base = (altair.Chart(frame[["Input Size", "Ratio"]]).mark_circle(opacity=0.5)
            .encode(x="Input Size:Q", y=altair.Y("Ratio:Q", scale=altair.Scale(domainMin=0)),
                    tooltip=[altair.Tooltip("Input Size", format=","),
                             altair.Tooltip("Ratio", format=",.2f")]))

    line = (base.transform_regression("Input Size", "Ratio")
            .mark_line())
    chart = (base + line).properties(
        title=title,
        width=800,
        height=525
    ).interactive()

    save_it(chart, filename)
    return

def swap_runner(swapper_one: Callable, swapper_two: Callable,
                label_one: str, label_two: str,
                things_to_partition: List[List],
                title: str, filename: str, plotter: Callable=swap_plots) -> None:
    """Run the partitioners and plot

    Args:
     swapper_one, swapper_two: swap-counter functions
     label_one, label_two: algorithm labels for the plot
     things_to_partition: collections for the partitioners to partition
     title, filename: plot strings
    """
    first_output = Parallel(n_jobs=-1)(
    delayed(swap_counter)(thing_to_partition, swapper_one)
    for thing_to_partition in things_to_partition)

    second_output = Parallel(n_jobs=-1)(
        delayed(swap_counter)(thing_to_partition, swapper_two)
        for thing_to_partition in things_to_partition)

    plotter(first_output, second_output, label_one, label_two,
            title=title,
            filename=filename)
    return

Random Inputs

counts = range(10, 100011, 100)
random_things_to_partition = [random.choices(range(count), k=count)
                              for count in counts]
swap_runner(levitin_swaps, clrs_swaps, "Levitin", "CLRS", random_things_to_partition,
           title="Levitin vs CLRS Partition Swap Count (Randomized Input)",
           filename="swaps_random_2")

Figure Missing

 
swap_runner(clrs_swaps, levitin_swaps, "CLRS", "Levitin", random_things_to_partition,
            title="CLRS/Levitin Partition Swap Ratio (Randomized Input)",
            filename="swaps_random_ratio", plotter=swap_ratio_plots)

Figure Missing

Biggest Item Last

What happens if the input has the biggest item at the end of the list?

counts = range(10, 100011, 100)
big_ended_things_to_partition = [random.choices(range(count), k=count) + [count]
                                 for count in counts]

swap_runner(levitin_swaps, clrs_swaps, "Levitin", "CLRS",
            big_ended_things_to_partition,
           title="Levitin vs CLRS Partition Swap Count (Biggest Item Last)",
           filename="swaps_sorted")

Figure Missing

Sorted

What happens if the input is already sorted?

counts = range(10, 100011, 100)
sorted_things_to_partition = [list(range(count)) for count in counts]

swap_runner(levitin_swaps, clrs_swaps, "Levitin", "CLRS",
            sorted_things_to_partition,
            title="Levitin vs CLRS Partition Swap Count (Sorted input)",
           filename="swaps_already_sorted")

Figure Missing

All The Same

counts = range(10, 100011, 100)
same_things_to_partition = [[count] * count for count in counts]

swap_runner(clrs_swaps, levitin_swaps, "CLRS", "Levitin", same_things_to_partition,
           title="Levitin vs CLRS Partition Swap Count (All Same Input)",
           filename="swaps_all_same")

Figure Missing

 
swap_runner(clrs_swaps, levitin_swaps,"CLRS", "Levitin", same_things_to_partition,
           title="CLRS/Levitin Partition Swap Ratio (All Same Input)",
           filename="swaps_all_same_ratio", plotter=swap_ratio_plots)

Figure Missing

Randomized Swaps

A Randomized Swap Counter

def randomized_swaps(collection: MutableSequence[Orderable],
                     partition: Callable, pivot: int) -> int:
    """Partitions the collection around the last element

    Args:
     collection: the list to partition
     partition: function to partition the list
     pivot: index of the element used for the pivot

    Returns:
     count of swaps
    """
    random_index = random.randrange(len(collection))
    collection[pivot], collection[random_index] = (collection[random_index],
                                                   collection[pivot])
    return 1 + partition(collection)

randomized_levitin = partial(randomized_swaps, partition=levitin_swaps, pivot=0)
randomized_clrs = partial(randomized_swaps, partition=clrs_swaps, pivot=-1)

Randomized Levitin Swaps

Shuffled Input

swap_runner(levitin_swaps, randomized_levitin, "Levitin", "Randomized Levitin",
            random_things_to_partition,
           title="Levitin vs Randomized Levitin Partition Swap Count (Randomized Input)",
           filename="swaps_randomized_random")

Figure Missing

Smallest Item At the End

counts = range(10, 100011, 100)
backwards_things_to_partition = [random.choices(range(1, count), k=count) + [0]
                                 for count in counts]

swap_runner(levitin_swaps, randomized_levitin, "Levitin", "Randomized Levitin",
            backwards_things_to_partition,
            title=("Levitin vs Randomized Levitin Partition Swap Count (Backwards Input)"),
            filename="swaps_levitin_randomized_sorted_backwards")

Figure Missing

All The Same Input

Since only difference between the randomized and the non-randomized input is that the pivot was (probably) swapped out, the input will look the same when all the values are the same to start with so I'm not going to re-plot those.

Randomized CLRS Swaps

Shuffled Input

swap_runner(clrs_swaps, randomized_clrs, "CLRS", "Randomized CLRS",
            random_things_to_partition,
           title="CLRS vs Randomized CLRS Partition Swap Count (Randomized Input)",
           filename="swaps_randomized_clrs_random")

Figure Missing

Biggest Item at the End

swap_runner(clrs_swaps, randomized_clrs, "CLRS", "Randomized CLRS",
            big_ended_things_to_partition,
            title="CLRS vs Randomized CLRS Partition Swap Count (Big-Ended Input)",
            filename="swaps_clrs_randomized_big_ended")

Figure Missing

Sorted

swap_runner(clrs_swaps, randomized_clrs, "CLRS", "Randomized CLRS",
            sorted_things_to_partition,
            title="CLRS vs Randomized CLRS Partition Swap Count (Sorted Input)",
            filename="swaps_clrs_randomized_sorted")

Figure Missing

CLRS Partition

Introduction

This is part of a series that starts with this post.

Imports and Setup

# python
from collections.abc import MutableSequence
from functools import partial

import random

# pypi
from expects import be_true, contain_exactly, equal, expect

import altair
import pandas

# software under test
from bowling.sort.quick import clrs_partition

# monkey
from graeae.visualization.altair_helpers import output_path, save_chart

SLUG = "clrs-partition"
OUTPUT_PATH = output_path(SLUG)
save_it = partial(save_chart, output_path=OUTPUT_PATH)

The Algorithm

The CLRS version seems a little clearer to follow although they use the last element as the pivot element instead of the first which threw me off for a bit. It uses a single for loop which moves anything less than the pivot element to the lower partition as it traverses the elements.

\begin{algorithm}
\caption{Partition (CLRS)}
\begin{algorithmic}
\INPUT An array and left and right locations defining a subarray
\OUTPUT The sub-array from left to right is partitioned and the partition location is returned

\PROCEDURE{Partition}{A, left, right}

\STATE PivotElement $\gets$ A[right]
\STATE LowerBound $\gets$ left - 1

\FOR {UpperBound $\in$ \{left $\ldots$ right - 1\}}
 \IF {A[UpperBound] $\leq$ PivotElement}
   \STATE LowerBound = LowerBound + 1
   \STATE \textsc{Swap}(A[LowerBound], A[UpperBound])
 \ENDIF
\ENDFOR

\STATE pivot $\gets$ LowerBound + 1
\STATE \textsc{Swap}(A[pivot], A[right])
\RETURN pivot
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

The LowerBound is the index of the last element less than or equal to the pivot and LowerBound + 1 is the first element greater than the pivot. The UpperBound is the index of the last item greater than the pivot.

The LowerBound is like a demon that guards the lower partition and the UpperBound is another demon that plows through the array, throwing any elements that belong in the lower partition back to the LowerBound demon who throws the first element in the upper partition back up to the UpperBound and moves up to guard the expanded lower partition.

A Worked Example

We can take a look at how this works using a table. I'll use LB for the LowerBound index, UB for the UpperBound index, and x for the PivotElement to keep the table from getting too wide (hopefully). The array to partition is [5, 7, 9, 4, 6] with a zero-based index so left = 0, right = 4 and x (the pivot element) is 6.

Here are the values for the variables as we step through the for-loop.

UB A[UB] A[UB] \(\leq\) x LB A
0 5 True 0 5, 7, 9, 4, 6
1 7 False 0 5, 7, 9, 4, 6
2 9 False 0 5, 7, 9, 4, 6
3 4 True 1 5, 4, 9, 7, 6

As long and the element in the array we're checking is less than or equal to the Pivot Element we increment the LowerBound along with the Upper Bound since the element belongs in the lower partition. If the Lower and Upper bound indexes are equal, than they agree on where it is so nothing happens when we do the swap (or you could say they swap in place, maybe). But while the element checked is larger than the Pivot Element the Upper Bound Index goes up but the Lower Bound doesn't so when we next hit a case where the element is less than or equal to the Pivot Element, we know it's out of place and needs to be swapped with the element currently just after the lower partition.

Once we're out of the loop we then swap out the Pivot Element and the element to the right of the Lower Bound (so the first element of the Upper Bound) and return the location where the Pivot Element ended up.

  • pivot = 2
  • A = [5, 4, 6, 7, 9]

An Odd Case

What happens if the last element is the largest element?

  • A = [9, 6, 25, 4, 100]
  • x = 100
UB A[UB] A[UB] \(\leq\) x LB A
0 9 True 0 9, 6, 25, 4, 100
1 6 True 1 9, 6, 25, 4, 100
2 25 True 2 9, 6, 25, 4, 100
3 4 True 3 9, 6, 25, 4, 100

And in the end we have a pivot of \(LB + 1 = 4\) (the last element) with the lower partition being everything but the last element and no elements in the upper partition. If the array happened to be already sorted than any attempt to partition a sub-array would end up with a similar output with an empty upper partition. This doesn't really matter here, but when we use it in quicksort it will.

Since nothing happens when an element being checked is greater than the pivot element, if the pivot element happens to be the smallest item in the array we'd have a similar case with an empty lower partition, the pivot element as the first element, and the rest of the elements in the upper partition, so starting with an array that's in reversed-sorted-order would also always end up with empty partitions no matter how we choose the sub-arrays.

The Implementation

According to wikipedia, the version CLRS uses is a version of the Lomuto Partition Scheme, created by Nico Lomuto.

def partition_clrs(collection: MutableSequence, left: int, right: int) -> int:
    """Partitions the collection around the last element

    Args:
     collection: the list to partition
     left: index of the first element in the sub-list to partition
     right: index of the last element in the sub-list to partition

    Returns:
     the index of the pivot element
    """
    pivot_element = collection[right]
    lower_bound = left - 1
    for upper_bound in range(left, right):
        if collection[upper_bound] <= pivot_element:
            lower_bound += 1
            (collection[lower_bound],
             collection[upper_bound]) = (collection[upper_bound],
                                         collection[lower_bound])
    pivot = lower_bound + 1
    (collection[pivot],
     collection[right]) = (collection[right],
                           collection[pivot])
    return pivot

Some Checks

The First Example

This is the worked example I gave.

start = [5, 7, 9, 4, 6]
test = start.copy()
expected = [5, 4, 6, 7, 9]
first_expected_pivot = 2

pivot = clrs_partition(test, 0, 4)

expect(pivot).to(equal(first_expected_pivot))
expect(test).to(contain_exactly(*expected))

And to make sure the sub-list works (as opposed to using the whole list).

left, right = [100, 20], [999, 888, 777]
test = left + start.copy() + right

pivot = clrs_partition(test, 2, 6)

# all we did was shift the sub-list to spots to the right
expect(pivot).to(equal(first_expected_pivot + 2))

# only the sub-list should be partitioned
expect(test).to(contain_exactly(*(left + expected + right)))

The Pivot Is the Biggest Element

If the last element (the pivot) is the biggest element then partitioning doesn't do anything to the list.

start = [9, 6, 25, 4, 100]
test = start.copy()

pivot = clrs_partition(test, 0, 4)

# the pivot should be the last element
expect(pivot).to(equal(4))

# nothing changes in the list
expect(test).to(contain_exactly(*start))

Small Inputs

Make sure it can handle collections of small size.

start = [0]
pivot = clrs_partition(start, 0, 0)
expect(pivot).to(equal(0))

start = [1, 2]
pivot = clrs_partition(start, 0, 1)
expect(pivot).to(equal(1))

Big Inputs

This is the same test as given to the Levitin version except we need to move the test-value to the end of the input list.

prefix = random.choices(range(100), k=100)
middle = 100
suffix = random.choices(range(101, 201), k=100)
test = prefix + suffix + [middle]

output = clrs_partition(test, 0, len(test) - 1)
expect(output).to(equal(middle))
expect(test[output]).to(equal(middle))
expect(all(item < middle for item in test[:output])).to(be_true)
expect(all(item > middle for item in test[output + 1:])).to(be_true)

A CLRS Tracker

This should be the same function (as clrs_partition) but it collects the locations of the elements within the list as they get swapped around.

def partition_tracker(collection: MutableSequence, 
                      left: int, right: int) -> tuple:
    """Partitions the collection around the last element

    Args:
     collection: the list to partition
     left: index of the first element in the sub-list to partition
     right: index of the last element in the sub-list to partition

    Returns:
     locations dict, lower_bounds, upper_bounds
    """
    locations = {value: [index] for index, value in enumerate(collection)}

    pivot_element = collection[right]
    lower_bound = left - 1

    lower_bounds = [lower_bound]
    for upper_bound in range(left, right):
        if collection[upper_bound] <= pivot_element:
            lower_bound += 1
            (collection[lower_bound],
             collection[upper_bound]) = (collection[upper_bound],
                                         collection[lower_bound])
        for index, item in enumerate(collection):
            locations[item].append(index)
        lower_bounds.append(lower_bound)
    pivot = lower_bound + 1
    (collection[pivot],
     collection[right]) = (collection[right],
                           collection[pivot])
    for index, item in enumerate(collection):
        locations[item].append(index)
    lower_bounds.append(lower_bound)
    return locations, lower_bounds

def partition_track_plotter(locations, lower_bounds, title, filename):
    frame = pandas.DataFrame(locations)
    re_indexed = frame.reset_index().rename(columns={"index": "Step"})

    melted = re_indexed.melt(id_vars=["Step"], var_name="Element",
                             value_name="Location")

    lower_frame = pandas.DataFrame({"Lower Bound": lower_bounds})
    re_lowered = lower_frame.reset_index().rename(columns={"index": "Step"})
    low_melted = re_lowered.melt(id_vars=["Step"], var_name="Element",
                                 value_name="Location")


    last_location = melted.Location.max()

    elements = altair.Chart(melted).mark_line().encode(
        x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
        y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
                   scale=altair.Scale(domain=(-1, last_location))),
        color=altair.Color("Element:O", legend=None),
        tooltip=["Step", "Element", "Location"]
    )

    lower = altair.Chart(low_melted).mark_line(color="red").encode(
        x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
        y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
                   scale=altair.Scale(domain=(-1, last_location))),
        tooltip=["Step", "Location"]
    )

    chart = (elements + lower).properties(
        title=title,
        width=800, height=520
    )

    save_it(chart, filename)
    return

A Backwards Case

First, a plot of a list that starts out with all the elements greater than the pivot followed by all the elements less than the pivot.

middle = 20
first_half = list(range(middle))
second_half = list(range(middle + 1, 2 * middle))

random.shuffle(first_half)
random.shuffle(second_half
)
items = second_half + first_half + [middle]

locations, lower_bounds = partition_tracker(items, 0, len(items) - 1)

partition_track_plotter(locations, lower_bounds, "CLRS Worst-Case Swapping", "clrs-worst-case")

Figure Missing

What we have here is that the first half of the steps are going over the items greater than the pivot so we never get past the conditional in the loop, thus nothing gets moved around. Then at the halfway point we start going over all the items bigger than the pivot so every item from that point gets swapped to the lower partition. Then in the final step we're out of the loop and the pivot gets moved to the middle of the partitions.

The red-line marks the last item in the lower partition. Even though I randomized the items, since we aren't sorting the values, just moving them backwards and forwards around the partitioning, it doesn't affect what happens.

A More Random Case

Let's try something a little more random.

middle = 20
first_half = list(range(middle))
second_half = list(range(middle + 1, 2 * middle))
items = first_half + second_half
random.shuffle(items)
items.append(middle)

locations, lower_bounds = partition_tracker(items, 0, len(items) - 1)

partition_track_plotter(locations, lower_bounds,
                        title="Randomized Input",
                        filename="partitioning-plot")

Figure Missing

Not a whole lot more interesting, but it shows how it normally works with the function moving things that have a lower value than the pivot element down to where the red line is (indicating the lower partition) whenever it's encountered as the loop is traversed, then at the end the pivot element gets swapped with the element that's just above the red line.

Sources

Levitin's Partition

Introduction

This is part of a series that starts with this post.

The Algorithm

The Levitin version of the Partition function is a little more complicated than the CLRS version. It uses an outer loop with two inner loops. The outer loop continues until the indices for the partitions cross-over (or meet) and the inner loops move the boundaries until they find a value that needs to be swapped to the other partition (e.g. the loop sweeping upwards finds an element that's greater than or equal to the pivot element and so it needs to be moved to the upper partition). It uses the first element in the array as the value around which to partition the array.

\begin{algorithm}
\caption{Partition (Levitin)}
\begin{algorithmic}
\INPUT An array and left and right locations defining a subarray
\OUTPUT The sub-array from left to right is partitioned and the partition location is returned

\PROCEDURE{Partition}{A, left, right}

\STATE PivotElement $\gets$ A[left]
\STATE PartitionLeft $\gets$ left
\STATE PartitionRight $\gets$ right + 1
\STATE \\
\REPEAT
  \REPEAT
    \STATE PartitionLeft $\gets$ PartitionLeft + 1
  \UNTIL {A[PartitionLeft] $\geq$ PivotElement}
  \STATE \\
  \REPEAT
    \STATE PartitionRight $\gets$ PartitionRight - 1
  \UNTIL {A[PartitionRight] $\leq$ PivotElement}

  \STATE \\ Swap(A[PartitionLeft], A[PartitionRight])

\UNTIL {PartitionLeft $\geq$ PartitionRight}
\STATE \\ Swap(A[PartitionLeft], A[PartitionRight])
\STATE Swap(A[left], A[PartitionRight])

\RETURN PartitionRight
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

The Implementation

Imports

# python
from collections.abc import MutableSequence
from functools import partial

import random

# pypi
from expects import be_true, contain_exactly, equal, expect

import altair
import pandas

# software under test
from bowling.sort.quick import levitins_partition

# monkey
from graeae.visualization.altair_helpers import output_path, save_chart

SLUG = "levitins-partition"
OUTPUT_PATH = output_path(SLUG)
save_it = partial(save_chart, output_path=OUTPUT_PATH)

The version Levitin uses appears to be closer to the version given by Tony Hoare, the creator of Quicksort. A notable difference between Wikipedia's pseudocode for Hoare's version and this version is that Hoare uses the middle element in the sub-array as the pivot while Levitin uses the left-most element as the pivot.

def partition_levitin(collection: MutableSequence,
                      left: int, right: int) -> int:
    """Partitions the collection around the first element

    Args:
     collection: the list to partition
     left: index of the first element in the sub-list to partition
     right: index of the last element in the sub-list to partition

    Returns:
     the index of the pivot element
    """
    pivot_element = collection[left]
    partition_left = left
    partition_right = right + 1

    while True:
        # if the pivot element is the largest element this loop
        # will try to go past the end of the list so we need a
        # check in the loop before we increment the partition_left
        while partition_left < right:
            partition_left += 1
            if collection[partition_left] >= pivot_element:
                break

        while True:
            partition_right -= 1
            if collection[partition_right] <= pivot_element:
                break

        if partition_left >= partition_right:
            break

        collection[partition_left], collection[partition_right] = (
            collection[partition_right], collection[partition_left]
        )

    # move the pivot element from the far left to its final place
    collection[left], collection[partition_right] = (
        collection[partition_right], collection[left]
    )

    return partition_right

Some Checks

start = [8, 9, 7]
output = levitins_partition(start, 0, 2)
expect(output).to(equal(1))
expect(start).to(contain_exactly(7, 8, 9))

start = [9, 9, 9 ,9, 9]
output = levitins_partition(start, 0, 3)
expect(output).to(equal(len(start)//2))

start = [0, 1, 2, 3, 4, 5]
output = levitins_partition(start, 0, 5)
expect(output).to(equal(0))
expect(start).to(contain_exactly(0, 1, 2, 3, 4, 5))

start = [5, 4, 3, 2, 1, 0]
output = levitins_partition(start, 0, 5)
expect(output).to(equal(5))
expect(start).to(contain_exactly(0, 4, 3, 2, 1, 5))

prefix = random.choices(range(100), k=100)
middle = 100
suffix = random.choices(range(101, 201), k=100)
test = [middle] + prefix + suffix

output = levitins_partition(test, 0, len(test) - 1)
expect(output).to(equal(middle))
expect(test[output]).to(equal(middle))
expect(all(item < middle for item in test[:output])).to(be_true)
expect(all(item > middle for item in test[output + 1:])).to(be_true)

A Levitin Tracker

This is the same function (hopefully) as levitins_partition but it collects the position of the elements in the list as things get swapped around so that we can plot it.

def levitin_tracker(collection: MutableSequence, 
                    left: int, right: int) -> tuple:
    """Partitions the collection around the last element

    Args:
     collection: the list to partition
     left: index of the first element in the sub-list to partition
     right: index of the last element in the sub-list to partition

    Returns:
     locations dict, lower_bounds, upper_bounds
    """
    # for the plotting
    locations = {value: [index] for index, value in enumerate(collection)}
    upper_bound = right
    lower_bound = left

    lower_bounds = [lower_bound]
    upper_bounds = [upper_bound]

    # the algorithm
    pivot_element = collection[left]
    partition_left = left
    partition_right = right + 1

    while True:
        while partition_left < right:
            partition_left += 1
            if collection[partition_left] >= pivot_element:
                break

        while True:
            partition_right -= 1
            if collection[partition_right] <= pivot_element:
                break

        if partition_left >= partition_right:
            break

        collection[partition_left], collection[partition_right] = (
            collection[partition_right], collection[partition_left]
        )

        # update the plotting
        upper_bounds.append(partition_right)
        lower_bounds.append(partition_left)
        for index, value in enumerate(collection):
            locations[value].append(index)

    collection[left], collection[partition_right] = (
        collection[partition_right], collection[left]
    )

    # update the plotting
    upper_bounds.append(partition_right)
    lower_bounds.append(partition_left)
    for index, value in enumerate(collection):
        locations[value].append(index)

    return locations, lower_bounds, upper_bounds

def levitin_track_plotter(locations, lower_bounds, upper_bounds, title, filename):
    frame = pandas.DataFrame(locations)
    re_indexed = frame.reset_index().rename(columns={"index": "Step"})

    melted = re_indexed.melt(id_vars=["Step"], var_name="Element",
                             value_name="Location")

    lower_frame = pandas.DataFrame({"Lower Bound": lower_bounds})
    re_lowered = lower_frame.reset_index().rename(columns={"index": "Step"})
    low_melted = re_lowered.melt(id_vars=["Step"], var_name="Element",
                                 value_name="Location")

    upper_frame = pandas.DataFrame({"Lower Bound": upper_bounds})
    re_uppered = upper_frame.reset_index().rename(columns={"index": "Step"})
    up_melted = re_uppered.melt(id_vars=["Step"], var_name="Element",
                                value_name="Location")

    last_location = melted.Location.max()

    elements = altair.Chart(melted).mark_line().encode(
        x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
        y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
                   scale=altair.Scale(domain=(-1, last_location))),
        color=altair.Color("Element:O", legend=None),
        tooltip=["Step", "Element", "Location"]
    )

    lower = altair.Chart(low_melted).mark_line(color="red").encode(
        x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
        y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
                   scale=altair.Scale(domain=(-1, last_location))),
        tooltip=["Step", "Location"]
    )

    upper = altair.Chart(up_melted).mark_line(color="red").encode(
        x=altair.X("Step:Q", axis=altair.Axis(tickMinStep=1)),
        y=altair.Y("Location:Q", axis=altair.Axis(tickMinStep=1),
                   scale=altair.Scale(domain=(-1, last_location))),
        tooltip=["Step", "Location"]
    )

    chart = (elements + lower + upper).properties(
        title=title,
    width=800, height=520
    )

    save_it(chart, filename)
    return

A Backwards Case

middle = 20
first_half = list(range(middle))
second_half = list(range(middle + 1, 2 * middle))

random.shuffle(first_half)
random.shuffle(second_half)

items = [middle] + second_half + first_half

locations, lower_bounds, upper_bounds = levitin_tracker(items, 0, len(items) - 1)
levitin_track_plotter(locations, lower_bounds, upper_bounds,
                      "Levitin Worst Case Swaps", "levitin-worst-plot")

Figure Missing

A More Random Case

Let's try something a little more random.

middle = 20
first_half = list(range(middle))
second_half = list(range(middle + 1, 2 * middle))
items = first_half + second_half
random.shuffle(items)
items.append(middle)

locations, lower_bounds, upper_bounds = levitin_tracker(items, 0, len(items) - 1)
levitin_track_plotter(locations, lower_bounds, upper_bounds,
                      title="Randomized Input", filename="levitin-randomized-input")

Figure Missing

A Sketch Of The Implementation

nil

Sources